Основания равнобокой трапеции равны 4 см и 12 см, а диагональ делит ее тупой угол пополам. Найдите площадь трапеции.

288

461

Посмотреть ответы 2

Ответы на вопрос:

EleonoraPonich

Геометрия

4,6(64 оценок)

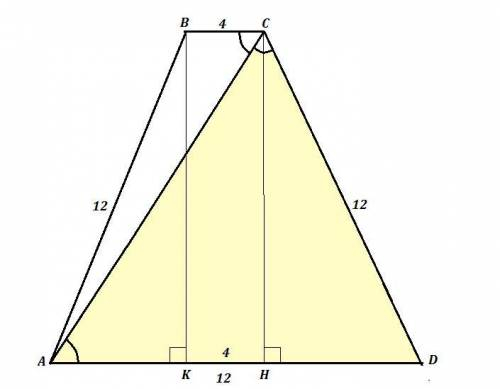
Трапеция АВCD - равнобокая, АВ=CD .

Основания АD=12 cм , BC=4 см .

АС - биссектриса ⇒ ∠АСВ=∠АСD .

Так как ВС || AD и АС - секущая , то ∠АСВ=∠САD как внутренние накрест лежащие углы .

Но по условию ∠АСВ=∠АСD , значит ∠САD=∠ACD и

ΔACD - равнобедренный , AD=CD=12 см . Тогда и АВ=CD=12 cм .

Опустим перпендикуляры из вершин В и С на АD , ВК⊥AD , CH⊥AD .

Тогда ВСНК - прямоугольник и ВС=КН=4 см .

ΔАВК = ΔCDH по гипотенузе (CD=AB) и острому углу (∠А=∠D как углы при основании равнобедренной трапеции) ⇒ АК=DH .

АК=DH=(AD-КН):2=(12-4):2=4 (см)

По теореме Пифагора найдём высоту трапеции из ΔCDH :

CD²=CH²+DH² ⇒ CH²=CD²-DH²=12²-4²144-16=128 ,

CH=√128=8√2 (см)

Площадь трапеции равна

S = (AD+BC):2*CH = (12+4):2*8√2 = 64√2 (см²)

Эльза132004

Геометрия

4,7(28 оценок)

13 ед.

Объяснение:

АВ=√(АС²+ВС²)=√(100+576)=√676=26.

АD=BD=26^2=13

Медиана прямоугольного треугольника равна половине гипотенузы.

х=13 ед.

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.