Алгебра: доказать тождество,задача на фото

000КапралЛеви000

01.02.2023 04:51

Алгебра

Есть ответ 👍

доказать тождество,задача на фото

252

329

Посмотреть ответы 2

Ответы на вопрос:

MaliaCr

Алгебра

4,8(39 оценок)

Доказать тождество .

$\displaystyle \bf \Big(1+\frac{1}{cos2a}+tg\, 2a\Big)\Big(1-\frac{1}{cos2a}+tg\, 2a\Big)=2\, tg\, 2a$

Применяем формулы косинуса и синуса двойных углов :

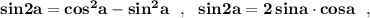$\bf sin2a=cos^2a-sin^2a\ \ ,\ \ sin2a=2\, sina\cdot cosa\ \ ,$ а также тождество

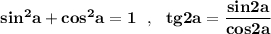$\bf sin^2a+cos^2a=1\ \ ,\ \ tg2a=\dfrac{sin2a}{cos2a}$ .

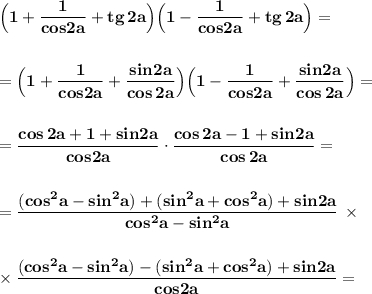
$\displaystyle \bf \Big(1+\frac{1}{cos2a}+tg\, 2a\Big)\Big(1-\frac{1}{cos2a}+tg\, 2a\Big)==\Big(1+\frac{1}{cos2a}+\frac{sin2a}{cos\, 2a}\Big)\Big(1-\frac{1}{cos2a}+\frac{sin2a}{cos\, 2a}\Big)==\frac{cos\, 2a+1+sin2a}{cos2a}\cdot \frac{cos\, 2a-1+sin2a}{cos\, 2a}==\frac{(cos^2a-sin^2a)+(sin^2a+cos^2a)+sin2a}{cos^2a-sin^2a}\, \times times \frac{(cos^2a-sin^2a)- (sin^2a+cos^2a)+sin2a}{cos2a}=$

$\bf \displaystyle =\frac{2cos^2a-2sina\cdot cosa}{(cosa-sina)(cosa+sina)}\cdot \frac{-2sin^2a+2sia\cdot cosa}{cos2a}==\frac{2cosa\cdot (cosa-sina)}{(cosa-sina)(cosa+sina)}\cdot \frac{2sina\cdot (sina+cosa)}{cos2a}==\frac{2\cdot 2\, sina\cdot cosa}{cos2a}=\frac{2\cdot sin2a}{cos2a}=2\, tg\, 2a2\, tg\, 2a=2\, tg\, 2a$

Тождество доказано .

Nbveh1234567890

Алгебра

4,4(85 оценок)

Пояснення:

f(x)=x² M(1;5)

$\displaystyle\\F(x)=\frac{x^3}{3} +CM(1;5)\ \ \ \ \ \Rightarrow5=\frac{1^3}{3}+C5=\frac{1}{3} +CC=4\frac{2}{3}=\frac{14}{3}.\ \ \ \ \ \ \Rightarrow F(x)=\frac{x^3}{3} +\frac{14}{3} =\frac{x^3+14}{3} .$

Для функції f(x)=x^2 знайти первісну графік якої проходить через точку M (1;5)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.