Рассмотрим тетраэдр ABCD. Пусть M, N, P и Q являются серединами ребер AB, BC, CD и DA соответственно. Пусть R - это точка пересечения отрезков MQ и NP. Ваша задача - доказать, что линия AR перпендикулярна плоскости MNPQ.

130

391

Посмотреть ответы 2

Ответы на вопрос:

dora12345pandora

Геометрия

4,5(3 оценок)

Чтобы доказать, что линия AR перпендикулярна плоскости MNPQ, мы можем воспользоваться свойством параллелограмма и треугольника.

Обратимся к треугольнику AMQ. Поскольку M и N являются серединами сторон AB и BC соответственно, то отрезок MN параллелен и равен половине отрезка AC. А по свойству параллелограмма, диагонали параллелограмма делятся пополам. Таким образом, точка R, являющаяся точкой пересечения отрезков MQ и NP, является серединой отрезка AC.

Аналогичные рассуждения можно провести для треугольников BNP, CPM и DQN, и прийти к выводу, что точка R является серединой отрезков BD, CD и AD соответственно.

Таким образом, линия AR проходит через середины всех ребер тетраэдра ABCD, а значит, она является медианой этого тетраэдра. Поскольку медиана пересекает плоскость MNPQ в ее центре (точке пересечения медиан), то линия AR будет перпендикулярна этой плоскости.

Таким образом, мы доказали, что линия AR перпендикулярна плоскости MNPQ.

azarovandrey123

Геометрия

4,6(89 оценок)

8 см, 20 см.

Объяснение:

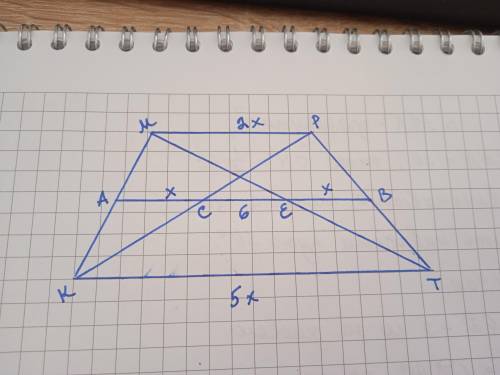
Дано: КМРТ - трапеція, АВ - середня лінія, СЕ=6 см. МР:КТ=2:5. Знайти МР і КТ.

Нехай МР=2х см, КТ=5х см.

Розглянемо ΔКМР та ΔМРТ. АС та ВЕ - середні лінії, АС=ВЕ=1/2 МР=х см.

Тоді АВ=2х+6 см.

Середня лінія трапеції дорівнює напівсумі основ, отже

2х+6=(2х+5х):2

2х+6=3,5х

1,5х=6; х=4.

МР=2*4=8 см; КТ=5*4=20 см

Основи трапеції пропорційні числам 2 і 5, а відрізок середньої лінії який лежить між діагоналями 6 с

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.