15.05.2021 22:24

Есть ответ 👍

Знайдіть найменший додатний корінь рівняння
1-sin 2x=(sin2x+cos 2x)^2

156

344

Посмотреть ответы 2

Ответы на вопрос:

лорею

Алгебра

4,7(100 оценок)

Наименьший положительный корень $\dfrac{\pi }{3}.$

Объяснение:

Найти наименьший положительный корень уравнения

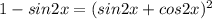
$1-sin2x=(sin2x+cos2x)^{2}$

Раскроем скобки в правой части уравнения, для этого применим формулу сокращенного умножения

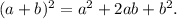
$(a+b)^{2} =a^{2} +2ab+b^{2} .$

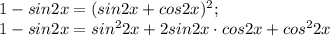
$1-sin2x=(sin2x+cos2x)^{2};\\1-sin2x=sin^{2} 2x+2sin2x\cdot cos2x+cos^{2} 2x$

Так как по основному тригонометрическому тождеству

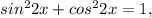
$sin^{2} 2x+cos^{2} 2x=1,$

то получим

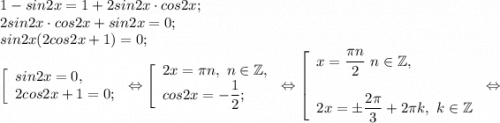
$1-sin2x=1+2sin2x\cdot cos2x;\\2sin2x\cdot cos2x+sin2x =0;\\sin2x( 2cos2x+1)=0;\\ \left [\begin{array}{l} sin2x = 0, \\ 2cos2x+1=0; \end{array} \right.\Leftrightarrow\left [\begin{array}{l} 2x = \pi n,~n\in\mathbb {Z}, \\ cos2x=-\dfrac{1}{2} ; \end{array} \right.\Leftrightarrow\left [\begin{array}{l} x = \dfrac{\pi n}{2} ~n\in\mathbb {Z}, \\ \\2x=\pm\dfrac{2\pi }{3}+2\pi k ,~k\in\mathbb {Z} \end{array} \right.\Leftrightarrow$

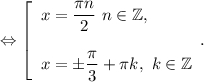
$\Leftrightarrow\left [\begin{array}{l} x = \dfrac{\pi n}{2} ~n\in\mathbb {Z}, \\ \\x=\pm\dfrac{\pi }{3}+\pi k ,~k\in\mathbb {Z} \end{array} .$

Найдем наименьший положительный корень.

1) При n = 1 получим положительный корень $x=\dfrac{\pi }{2}$

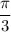2) При k=0 получим два корня $\pm\dfrac{\pi }{3}$ , но положительным будет $\dfrac{\pi }{3}$ .

Наименьшим будем корень $\dfrac{\pi }{3}.$

#SPJ1

alexaval1980p08mu0

Алгебра

4,8(88 оценок)

сори алгебру не

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.