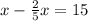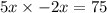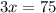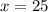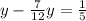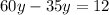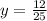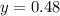vika03121

21.11.2022 19:17

Математика

Есть ответ 👍

Найдите наибольшее целое число,являющееся решением неравенства: 3) 7x - x^3 > 27x - (x+8)(x^2-8x+64)

205

252

Посмотреть ответы 3

Ответы на вопрос:

hvbdnnd

Математика

4,6(91 оценок)

Раскроем скобки во второй части неравенства и приведем подобные слагаемые:

7x - x^3 > 27x - x^3 - 8x^2 + 64x - 512

Сократим одинаковые слагаемые:

0 > 20x - 8x^2 + 512

Перенесем все слагаемые в левую часть и получим квадратное уравнение:

8x^2 - 20x + 512 < 0

Решим его с дискриминанта:

D = 20^2 - 48512 = -64512

Так как дискриминант отрицательный, то уравнение не имеет действительных корней.

Значит, неравенство не имеет решений, и ответ: нет решений.

Пошаговое объяснение:

alexa7021

Математика

4,7(22 оценок)

ответ:x = 6.

Пошаговое объяснение: Начнем с раскрытия скобок в правой части неравенства:

(x+8)(x^2-8x+64) = x^3 - 64

Подставляем это выражение в исходное неравенство:

7x - x^3 > 27x - (x^3 - 64)

x^3 - 20x > 64

x^3 > 20x + 64

Для нахождения наибольшего целого числа, удовлетворяющего этому неравенству, можно последовательно подставлять целые значения x начиная с наибольшего и проверять выполнение неравенства.

При x = 7:

7^3 > 20*7 + 64

343 > 204 + 64

343 > 268

Условие неравенства выполняется, значит x = 7 является решением.

При x = 6:

6^3 > 20*6 + 64

216 > 120 + 64

216 > 184

Условие неравенства также выполняется, значит x = 6 тоже является решением.

Однако, при x = 5:

5^3 > 20*5 + 64

125 > 100 + 64

125 > 164

Условие неравенства не выполняется, значит наибольшим целым числом, удовлетворяющим неравенству, является x=6.

Hedulik

Математика

4,8(84 оценок)

$x - \frac{2}{5} x = 15$

$5x \times - 2x = 75$

3x = 75

x = 25

ппп

$y - \frac{7}{12} y = \frac{1}{5}$

60y - 35y = 12

$y = \frac{12}{25}$

y = 0.48

сделай мой ответ лучшим

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.