В 7^А классе учится 20 человек, и все они очень любят многопользовательские компьютерные игры. Каждый из учащихся играет в одну или две таких игры. При этом для любых 2 учащихся найдется общая игра (в которую играют оба). Найдите наибольшее N, такое, что гарантированно найдется игра, в которую играют не менее N учащихся.
Ответы на вопрос:
Наибольшее число N, при котором гарантированно существует игра, в которую играют не менее N студентов, равно 20. Это объясняется тем, что если каждый студент играет в одну или две игры, и для любых двух студентов есть общая игра, то каждый студент должен играть хотя бы в одну игру, которая является общей для всех 20 студентов в классе. Поэтому наибольшее число N, при котором гарантированно найдется игра, в которую играют не менее N учеников, равно 20.
Пусть 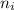 - число учащихся, которые играют в игру
- число учащихся, которые играют в игру  . Нужно отсортировать игры в порядке возрастания
. Нужно отсортировать игры в порядке возрастания 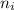 . Тогда мы можем получить следующую систему неравенств:
. Тогда мы можем получить следующую систему неравенств:


Где  - наибольший индекс, такой что
- наибольший индекс, такой что 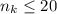 . В этой системе неравенств
. В этой системе неравенств  является наибольшим возможным числом учащихся, которые играют в одну из игр
является наибольшим возможным числом учащихся, которые играют в одну из игр 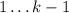 , а
, а 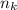 - число учащихся, которые играют только в игру
- число учащихся, которые играют только в игру  . Таким образом, наибольшее число
. Таким образом, наибольшее число  учащихся, которые играют в одну игру, равно
учащихся, которые играют в одну игру, равно  . Наша задача - найти наибольшее возможное значение
. Наша задача - найти наибольшее возможное значение  .
.
По условию, для любых двух учащихся найдется общая игра. Это означает, что для любой пары 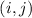 ,
, 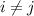 , выполняется условие
, выполняется условие 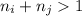 . Также из условия
. Также из условия  следует, что для любой пары
следует, что для любой пары 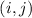 ,
, 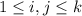 , выполняется условие
, выполняется условие 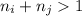 . Если мы присвоим значение
. Если мы присвоим значение 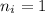 всем играм
всем играм  , то условия выше будут выполнены, но сумма
, то условия выше будут выполнены, но сумма 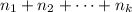 будет меньше
будет меньше 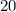 . Поэтому мы можем заметить, что если
. Поэтому мы можем заметить, что если 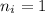 для некоторых
для некоторых  , то сумма
, то сумма 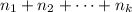 будет меньше
будет меньше 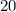 . Отсюда следует, что все игры
. Отсюда следует, что все игры  имеют
имеют  . Таким образом, наибольшее число учащихся, которые играют в одну игру, равно
. Таким образом, наибольшее число учащихся, которые играют в одну игру, равно  . Поскольку это число должно быть меньше
. Поскольку это число должно быть меньше 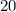 , то
, то 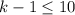 , что означает, что
, что означает, что  . Значит, наибольшее число
. Значит, наибольшее число  учащихся, которые играют в одну игру, равно
учащихся, которые играют в одну игру, равно  , где
, где  - наибольший индекс, такой что
- наибольший индекс, такой что 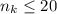 . Значит, наибольшее число
. Значит, наибольшее число  учащихся, которые играют в одну игру, равно
учащихся, которые играют в одну игру, равно 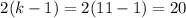 .
.
ответ: 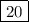 .
.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Кто понимает математику мне нужно это Бжб 17 мин осталось и подписываюсь в знак...
 Ьрнрг29.07.2021 05:20
Ьрнрг29.07.2021 05:20 -
Числа ті, 12, 13, 14 являются последовательными членами геометрической прогрессии...
 aiym1911.12.2020 02:12
aiym1911.12.2020 02:12 -
Знайдіть радіус кола якщо його діаметр 22см...
 mehili26.06.2022 08:12
mehili26.06.2022 08:12 -
Задание 1 Прочитай текст. Установи соответствие. Что за улица! Что за городок!...
 romashka189926.11.2021 12:02
romashka189926.11.2021 12:02 -
используя переместительное и сочетательное свойство Вычисли наиболее удобным жаю...
 Coffee199815.02.2022 23:59
Coffee199815.02.2022 23:59 -
Напишите линейную функцию, график которой перпендикулярен графику функции y = -2x...
 muhkirill201708.12.2022 15:36
muhkirill201708.12.2022 15:36 -
Отрезок, концы которого расположены в точках a(-4;2) b(8;-4) разделены на четыре...
 ChristmasNastya17.06.2022 20:46
ChristmasNastya17.06.2022 20:46 -
С меня лайки на все ответы ваши и подписка) Это СОР поэтому быстрее)...
 nooooovikovaaaaa34528.03.2022 02:21
nooooovikovaaaaa34528.03.2022 02:21 -
Запишите периодическую десятичную дробь в виде обыкновенной а) 3 (4) б) 2 3(7)...
 efr4703.05.2021 03:22
efr4703.05.2021 03:22 -
(1125+875)×18+4328+(976543-123459)×100столбиком ...
 donerkebab08.04.2020 09:59
donerkebab08.04.2020 09:59

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
