CTpeJIa333

01.10.2022 20:20

Математика

Есть ответ 👍

Дан ящик с квадратным основанием и объемом 64. Каковы должна быть его высота для того, чтобы поверхность без крышки была наименьшей? Умоляю

207

218

Посмотреть ответы 2

Ответы на вопрос:

сом03

Математика

4,8(43 оценок)

Высота должна быть равна $2\sqrt[3]{2}$

Пошаговое объяснение:

Пусть сторона основания равна x, тогда площадь основания 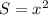$S = {x^2}$ .

Так как объем такой прямой призмы вычисляется по формуле 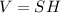V = SH , то

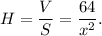
$H = \displaystyle\frac{V}{S} = \displaystyle\frac{{64}}{{{x^2}}}.$

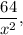Площадь поверхности без крышки состоит из четырех площадей одинаковых боковых граней, каждая из которых прямоугольник со сторонами и $\displaystyle\frac{{64}}{{{x^2}}},$ и площади основания (дна), поэтому она равна

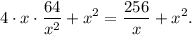
$4 \cdot x \cdot \displaystyle\frac{{64}}{{{x^2}}} + {x^2} = \displaystyle\frac{{256}}{x} + {x^2}.$

Найдем минимум функции

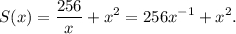
$S(x) = \displaystyle\frac{{256}}{x} + {x^2} = 256{x^{ - 1}} + {x^2}.$

Вычислим производную, применяя формулу $({x^n})' = n{x^{n - 1}},$ и приравняем ее нулю.

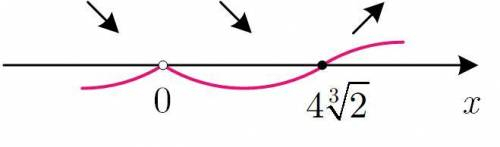
$S'(x) = - \displaystyle\frac{{256}}{{{x^2}}} + 2x = 0;displaystyle\frac{{2{x^3} - 256}}{{{x^2}}} = 0;2{x^3} = 256;{x^3} = 128;x = \sqrt[3]{{{2^7}}} = 4\sqrt[3]{2}.$

С метода интервалов убеждаемся, что проходя через эту точку производная меняет свой знак с минуса на плюс, таким образом, в этой точке достигается минимум функции.

При найденном значении высота равна

$H = \displaystyle\frac{{64}}{{{x^2}}}=\displaystyle\frac{{64}}{{{16\sqrt[3]{4=2\sqrt[3]{2}.$

Дан ящик с квадратным основанием и объемом 64. Каковы должна быть его высота для того, чтобы поверхн

Maxbys

Математика

4,4(92 оценок)

Восемь сорок девятых 8/49

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.