Алгебра: Найти остаток от деления 101^88+17×48^101+3 на 31

vovaq6oziu5d

19.11.2021 09:26

Есть ответ 👍

Найти остаток от деления 101^88+17×48^101+3 на 31

241

310

Посмотреть ответы 2

нвчббисмт

Алгебра

4,7(56 оценок)

Если к числу 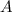прибавить (или отнять) некоторое количество раз число 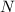, то полученное число будет равно числу 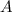по модулю :

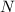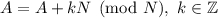
$A=A+kN\pmod{N},\ k\in\mathbb{Z}$

Числа, равные по модулю 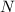, дают при делении на 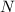равные остатки.

Преобразуем первое слагаемое:

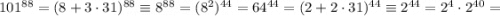
$101^{88}=(8+3\cdot31)^{88}\equiv8^{88}=(8^2)^{44}=64^{44}=(2+2\cdot31)^{44}\equiv2^{44}=2^4\cdot2^{40}=$

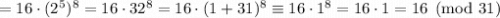
$=16\cdot(2^5)^8=16\cdot32^8=16\cdot(1+31)^8\equiv16\cdot1^8=16\cdot1=16\pmod{31}$

Преобразуем второе слагаемое:

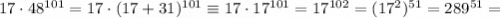
$17\cdot48^{101}=17\cdot(17+31)^{101}\equiv17\cdot17^{101}=17^{102}=(17^2)^{51}=289^{51}=$

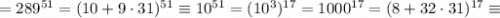
$=289^{51}=(10+9\cdot31)^{51}\equiv10^{51}=(10^3)^{17}=1000^{17}=(8+32\cdot31)^{17}\equiv$

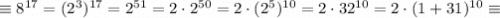
$\equiv8^{17}=(2^3)^{17}=2^{51}=2\cdot2^{50}=2\cdot(2^5)^{10}=2\cdot32^{10}=2\cdot(1+31)^{10}\equiv$

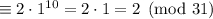
$\equiv2\cdot1^{10}=2\cdot1=2\pmod{31}$

Тогда, исходная сумма перепишется в виде:

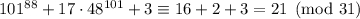
$101^{88}+17\cdot48^{101}+3\equiv16+2+3=21\pmod{31}$

Так как число 21 при делении на 31 дает остаток 21, то и исходное число, равное ему по модулю 31, также при делении на 31 дает остаток 21.

ответ: 21

cikitka2

Алгебра

4,7(79 оценок)

разложение

Объяснение:

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.