Математика: . С 5,6 и 7заданием!.

виталька1001

03.11.2020 15:51

Математика

Есть ответ 👍

. С 5,6 и 7заданием!.

138

473

Посмотреть ответы 2

Ответы на вопрос:

школьник62728474щ3

Математика

4,7(85 оценок)

5. –2, 1;

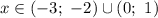6. $x \in ( - 3;\,\, - 2) \cup (0;\,\,1)$ ;

7. y = x + 1

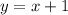
Пошаговое объяснение:

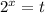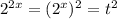5. Сделаем замену ${2^x} = t$ , тогда ${2^{2x}} = {({2^x})^2} = {t^2}$ .

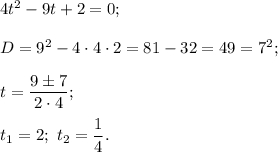
$4{t^2} - 9t + 2 = 0;D = {9^2} - 4 \cdot 4 \cdot 2 = 81 - 32 = 49 = {7^2};t = \displaystyle\frac{{9 \pm 7}}{{2 \cdot 4}};{t_1} = 2;\,\,{t_2} = \displaystyle\frac{1}{4}.$

Делаем обратную замену:

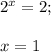
${2^x} = 2;x = 1$

либо

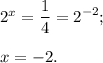
${2^x} = \displaystyle\frac{1}{4} = {2^{ - 2}};x = - 2.$

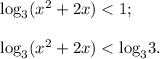
${\log _3}({x^2} + 2x) < 1;{\log _3}({x^2} + 2x) < {\log _3}3.$

Так как функция 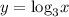$y = {\log _3}x$ возрастающая, то с возрастанием аргумента увеличивается и значение функции. Также учитывая положительность подлагорифмического выражения, получаем:

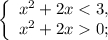
$\left\{ \begin{array}{l}{x^2} + 2x < 3,\\{x^2} + 2x 0;\end{array} \right.$

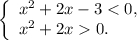
$\left\{ \begin{array}{l}{x^2} + 2x - 3 < 0,\\{x^2} + 2x 0.\end{array} \right.$

Корни первого квадратного трехчлена находим по теореме Виета:

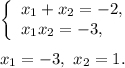
$\left\{ \begin{array}{l}{x_1} + {x_2} = - 2,\\{x_1}{x_2} = - 3,\end{array} \right.{x_1} = - 3,\,\,{x_2} = 1.$

Так как 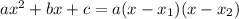$a{x^2} + bx + c = a(x - {x_1})(x - {x_2})$ , то

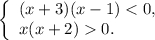
$\left\{ \begin{array}{l}(x + 3)(x - 1) < 0,\\x(x + 2) 0.\end{array} \right.$

Используя метод интервалов (дважды) для решения каждого из неравенств и объединяя их решения в систему (см. рис.), получаем ответ: 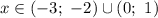$x \in ( - 3;\,\, - 2) \cup (0;\,\,1)$ .

7. Уравнение касательной в общем виде выглядит как 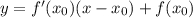$y = f'({x_0})(x - {x_0}) + f({x_0})$ .

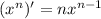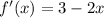С формулы $({x^n})' = n{x^{n - 1}}$ найдем производную функции: f'(x) = 3 - 2x .

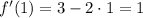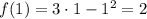Тогда $f'(1) = 3 - 2 \cdot 1 = 1$ ; $f(1) = 3 \cdot 1 - {1^2} = 2$ .

Значит уравнение касательной имеет вид: 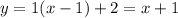y = 1(x - 1) + 2 = x + 1 .

kir1kir1

Математика

4,4(74 оценок)

x*x тип того это площадь квадрата

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.