26.10.2021 03:16

Есть ответ 👍

Сума катетів прямокутного трикутника дорівнює 70 см, а сума медіани і висоти, проведеної до гіпотенузи, - 49 см. Знайдіть периметр
трикутника.

209

405

Посмотреть ответы 3

Ответы на вопрос:

rogubankova

Геометрия

4,7(7 оценок)

Периметр треугольника равен 120 см

Объяснение:

Пусть один из катетов прямоугольного треугольника равен 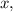тогда второй —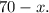 70 - x.

По теореме Пифагора гипотенуза такого треугольника равна

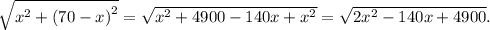
$\sqrt {{x^2} + {{(70 - x)}^2}} = \sqrt {{x^2} + 4900 - 140x + {x^2}} = \sqrt {2{x^2} - 140x + 4900} .$

В прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине, т. е.

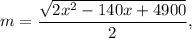
$m = \displaystyle\frac{{\sqrt {2{x^2} - 140x + 4900} }}{2},$

а высота, проведенная к гипотенузе, вычисляется через формулу 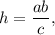$h = \displaystyle\frac{{ab}}{c},$ т. е.

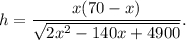
$h = \displaystyle\frac{{x(70 - x)}}{{\sqrt {2{x^2} - 140x + 4900} }}.$

По условию

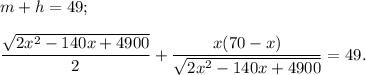
$m + h = 49;displaystyle\frac{{\sqrt {2{x^2} - 140x + 4900} }}{2} + \displaystyle\frac{{x(70 - x)}}{{\sqrt {2{x^2} - 140x + 4900} }} = 49.$

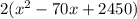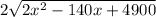Заметим, что дискриминант квадратного трехчлена $2({x^2} - 70x + 2450)$ отрицательный, значит выражение под корнем никогда не превращается в ноль. Умножим обе части уравнения на $2\sqrt {2{x^2} - 140x + 4900}$ :

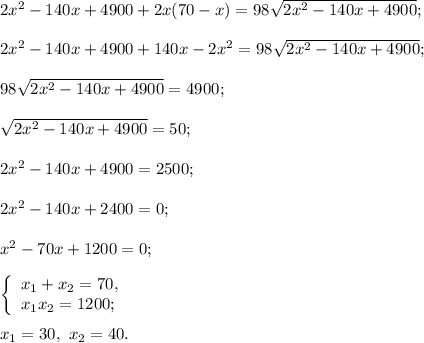
$2{x^2} - 140x + 4900 + 2x(70 - x) = 98\sqrt {2{x^2} - 140x + 4900} ;2{x^2} - 140x + 4900 + 140x - 2{x^2} = 98\sqrt {2{x^2} - 140x + 4900} ;98\sqrt {2{x^2} - 140x + 4900} = 4900;sqrt {2{x^2} - 140x + 4900} = 50;2{x^2} - 140x + 4900 = 2500;2{x^2} - 140x + 2400 = 0;{x^2} - 70x + 1200 = 0;left\{ \begin{array}{l}{x_1} + {x_2} = 70,\\{x_1}{x_2} = 1200;\end{array} \right.{x_1} = 30,\,\,{x_2} = 40.$

Значит катеты треугольника 30 и 40, а гипотенуза

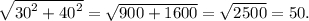
$\sqrt {{{30}^2} + {{40}^2}} = \sqrt {900 + 1600} = \sqrt {2500} = 50.$

Таким образом, периметр треугольника равен

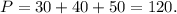
P = 30 + 40 + 50 = 120.

Виктория11618

Геометрия

4,8(34 оценок)

Периметр треугольника равен 120 см.

Объяснение:

Сумма катетов прямоугольного треугольника равна 70 см, а сумма медианы и высоты , проведенных к гипотенузе, равна 49 см . Найти периметр треугольника.

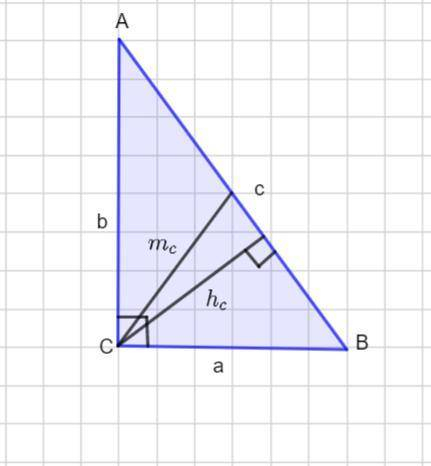
Пусть дан Δ АВС , в котором a и b - катеты , с - гипотенуза .

Тогда а+ b =70 см

Медиану, проведенную к гипотенузе, назовем 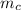$m{_c}$ , а высоту, проведенную к гипотенузе назовем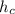 $h{_c}$

Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то 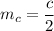$m{_c}= \dfrac{c}{2}$

Высота прямоугольного треугольника, проведенная к гипотенузе, определяется по формуле 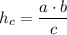$h{_c}= \dfrac{a\cdot b}{c}$

где a,b-катеты , c - гипотенуза.

По условию

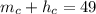$m{_c}+h{_c}= 49$ см

Тогда

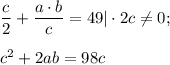$\dfrac{c}{2} +\dfrac{a\cdot b }{c} =49|\cdot 2c\neq 0 ;c^{2} +2ab =98c$ (1)

Теорема Пифагора : в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

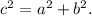
$c^{2} =a^{2} +b^{2} .$

Подставим в равенство (1) вместо 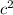$c^{2}$ выражение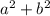 $a^{2} +b^{2}$

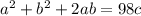
$a^{2} +b^{2} +2ab =98c$

Применим формулу сокращенного умножения

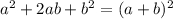
$a^{2} +2ab+b^{2} =(a+b)^{2}$

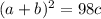
$(a+b)^{2}=98c$

По условию а+ b =70.

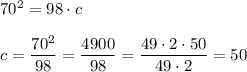
$70^{2} =98\cdot cc= \dfrac{70^{2} }{98} =\dfrac{4900}{98} =\dfrac{49\cdot2\cdot50 }{49\cdot2} =50$

Значит, гипотенуза с= 50 см.

Периметр треугольника - это сумма длин всех сторон .

Тогда P=a+b+c

P= 70 + 50 =120 cм

Сума катетів прямокутного трикутника дорівнює 70 см, а сума медіани і висоти, проведеної до гіпотену

PoliKotova02

Геометрия

4,5(70 оценок)

Ответ: r = 2

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.