Регистрация Спросить otvet5GPT
LizaPetukhova
26.06.2023 14:49
Математика
Есть ответ 👍

Площа ривнобедренного трикутника з кутом при основи 30 доривнюэ 64 корень из 3 см^2 Знайдить стороны трикутника

288
482
Посмотреть ответы 3

Ответы на вопрос:

iSlate999
iSlate999
4,8(34 оценок)

Так, як ΔАВС рівнобедрений позначимо бокові сторони, як х, а кут між ними: 180-(30*2)=180-60=120°

Площа трикутника знаходиться по формулі:

SΔ=(1/2)*х*х*sin120°=(1/2)*х² *(√3/2)

64√3=(1/2)*х² *(√3/2)

64√3=(√3/4)*х²

х²=256

х=16

АВ=ВС=16 см

Побудуємо висоту ВН, отримаємо прямокутний ΔАВН

За опорним фактом: ВН=1/2АВ=1/2*16=8 (см)

За теоремою Пифагора знайдемо АН:

АН=√(АВ²-ВН²)=√(16²-8²)=√(256-64)=√192=8√3 (см)

АС=2АН=(8√3)*2=16√3 (см)

Відповідь: сторони трикутника 16, 16 и 16√3.


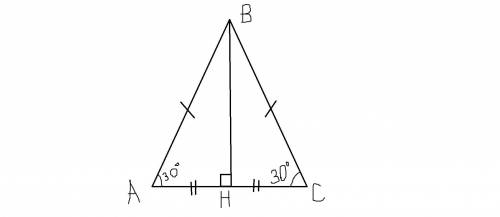
Площа ривнобедренного трикутника з кутом при основи 30 доривнюэ 64 корень из 3 см^2 Знайдить стороны
Ооооооокккккккк
Ооооооокккккккк
4,6(50 оценок)

16 см,16 см,  16√3 см.

Пошаговое объяснение:

Дано: ΔАВС, АВ=ВС,  ∠А=∠С=30°,  S(АВС)=64√3 см².  АВ - ?  ВС - ?  АС - ?

Проведемо висоту ВН, яка є медіаною та бісектрисою ΔАВС.

ΔАВН=ΔСВН (АВ=ВС;  ВН - спільна сторона;  АН=СН).

Розглянемо ΔАВН - прямокутний,  ∠А=30°,  отже ВН=1/2 АВ.

Нехай ВН=х см,  тоді АВ=2х см

За теоремою Піфагора (2х)²=(АС/2)²+х²;  4х²=АС²/4 + х²;  АС²/4=3х²;  АС=2х√3.

S(АВС)=1/2 * АС * ВН;  64√3 = 1/2 * 2х√3 * х;  

64√3=x²√3;   x²=64;    x=8.  ВН=8 см.

АВ=ВС=2*8=16 см,  АС=2*8*√3=16√3 см


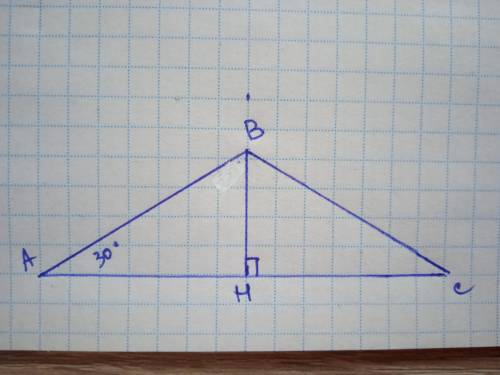
Площа ривнобедренного трикутника з кутом при основи 30 доривнюэ 64 корень из 3 см^2 Знайдить стороны
mishishinatany
mishishinatany
4,4(63 оценок)

ответ:
Глядя на фото мы понимаем , что во 2ой координатной четверти лежит точка Б(-7:2)

Надеюсь  я . Обращайся. (если можно ,то поставьте "лучший ответ" :)


яка з наведених точок лежить у II координатній чверті? А) А (7;-2), Б) В - (7;2), В) C (7;2), Г) D (

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS