Регистрация Спросить otvet5GPT
Ann1484
21.05.2021 17:04
Геометрия
Есть ответ 👍

В ромбе ABCD
AC больше BD и АС/BD - BD/AC = 2√3
Найдите угол A

280
346
Посмотреть ответы 2

Ответы на вопрос:

maz156
maz156
4,4(100 оценок)

\frac{\pi }{6}

Объяснение:

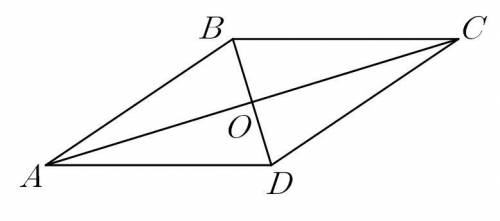
Информация, что диагональ ромба 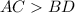AC BD говорит о том, что \angle A — острый.

Пусть 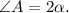\angle A = 2\alpha . Так как диагонали ромба являются биссектрисами его углов,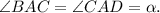 \angle BAC = \angle CAD = \alpha .

Из метрических соотношений в прямоугольном треугольнике

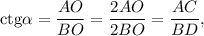
{\mathop{\rm ctg}\nolimits} \alpha = \displaystyle\frac{{AO}}{{BO}} = \displaystyle\frac{{2AO}}{{2BO}} = \displaystyle\frac{{AC}}{{BD}},

и наоборот,

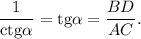
\displaystyle\frac{1}{{{\mathop{\rm ctg}\nolimits} \alpha }} = {\mathop{\rm tg}\nolimits} \alpha = \displaystyle\frac{{BD}}{{AC}}.

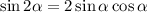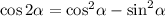Тогда по условию, а затем с применением формул синуса и косинуса двойного угла \sin 2\alpha = 2\sin \alpha \cos \alpha  и \cos 2\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha:

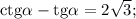
{\mathop{\rm ctg}\nolimits} \alpha - {\mathop{\rm tg}\nolimits} \alpha = 2\sqrt 3 ;\\

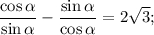
\displaystyle\frac{{\cos \alpha }}{{\sin \alpha }} - \displaystyle\frac{{\sin \alpha }}{{\cos \alpha }} = 2\sqrt 3 ;\\

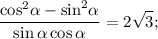
\displaystyle\frac\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\sin \alpha \cos \alpha }} = 2\sqrt 3 ;\\

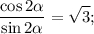
\displaystyle\frac{{\cos 2\alpha }}{{\sin 2\alpha }} = \sqrt 3 ;\\

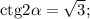
{\mathop{\rm ctg}\nolimits} 2\alpha = \sqrt 3 ;\\

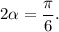
2\alpha = \displaystyle\frac{\pi }{6}.


В ромбе ABCD AC больше BD и АС/BD - BD/AC = 2√3 Найдите угол A
роолли
роолли
4,4(68 оценок)

Решение во вложении....


решить геометрию

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS