Доказать неравенство, если a>0, b>0, c>0
(Довести нерівність, якщо a>0, b>0, c>o)

140

320

Посмотреть ответы 2

Ответы на вопрос:

faiarina2016

Математика

4,8(79 оценок)

Нужно применить метод ранее доказанного неравенства:

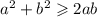
${a}^{2} + {b}^{2} \geqslant 2ab$

Из нее следует:

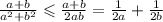
$\frac{a + b}{ {a}^{2} + {b}^{2} } \leqslant \frac{a + b}{2ab} = \frac{1}{2a} + \frac{1}{2b}$

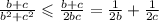
$\frac{b + c}{ {b}^{2} + {c}^{2} } \leqslant \frac{b + c}{2bc} = \frac{1}{2b} + \frac{1}{2c}$

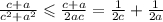
$\frac{c + a}{ {c}^{2} + {a}^{2} } \leqslant \frac{c + a}{2ac} = \frac{1}{2c} + \frac{1}{2a}$

Теперь по свойству почленного прибавления неравенств, получим :

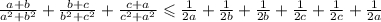
$\frac{a + b}{{a}^{2} + {b}^{2} } + \frac{b + c}{ {b}^{2} + {c}^{2} } + \frac{c + a}{ {c}^{2} + {a}^{2} } \leqslant \frac{1}{2a} + \frac{1}{2b} + \frac{1}{2b} + \frac{1}{2c} + \frac{1}{2c} + \frac{1}{2a}$

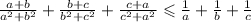
$\frac{a + b}{{a}^{2} + {b}^{2} } + \frac{b + c}{ {b}^{2} + {c}^{2} } + \frac{c + a}{ {c}^{2} + {a}^{2} } \leqslant \frac{1}{a} + \frac{1}{b} + \frac{1}{c}$

Доказано

данил1780

Математика

4,8(79 оценок)

Y' = tg⁸(x)/((m^2 + n^2)cos²(x))

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.