Регистрация Спросить otvet5GPT
zzz1792
26.08.2021 09:23
Математика
Есть ответ 👍

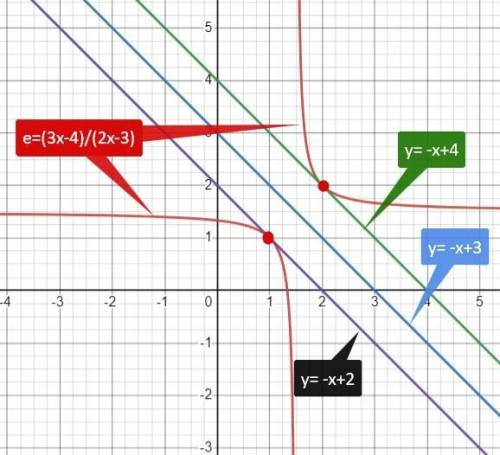
Найдите уравнение касательной к кривой y=3x-4/2x-3, параллельных прямой y=-x+3

119
201
Посмотреть ответы 2

Ответы на вопрос:

mirtovamasha
mirtovamasha
4,7(97 оценок)

уравнения касательных у₁ = -х + 2;  у₂ = -х + 4

Пошаговое объяснение:

Прежде всего найдем уравнение касательной.

Уравнение касательной имеет вид

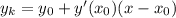
y_k = y_0 + y'(x_0)(x - x_0)

\displaystyle y'=\bigg(\frac{3x-4}{2x-3}\bigg) '=\bigg[\;\bigg(\frac{u}{v} \bigg)'=\frac{u'v-v'u}{v^2}\;\bigg] =

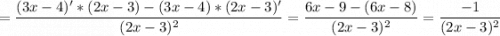
\displaystyle =\frac{(3x-4)'*(2x-3)-(3x-4)*(2x-3)'}{(2x-3)^2} =\frac{6x-9-(6x-8)}{(2x-3)^2} =\frac{-1}{(2x-3)^2}

Рассмотрим уравнение касательной  в точке х₀ (эту точку нам и надо найти)

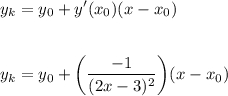
\displaystyle y_k = y_0 + y'(x_0)(x - x_0)y_k = y_0 + \bigg(\frac{-1}{(2x-3)^2}\bigg)(x - x_0)

Для того, чтобы две прямые были параллельны, необходимо,  чтобы в уравнениях прямых коэффициенты при х были бы равны.

У прямой у = -x + 3  коэффициент при х равен -1

У касательной коэффициент при х равен 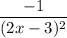  \displaystyle \frac{-1}{(2x-3)^2}

Приравняем коэффициенты и найдем х₀

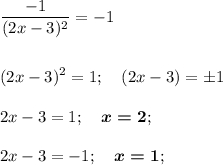
\displaystyle \frac{-1}{(2x-3)^2} =-1(2x-3)^2 = 1;\quad (2x-3)=\pm12x-3 = 1;\quad \boldsymbol {x= 2};2x-3 = -1;\quad \boldsymbol {x= 1};

Таким образом, у нас есть две точки касания, в которых касательная будет параллельна прямой у = -х +3

Найдем уравнение касательной в точке  х₀ = 1

Подставим  х₀ в формулу касательной.

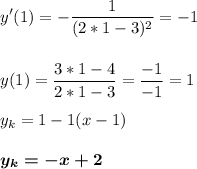\displaystyle y'( 1) = -\frac{1}{(2*1-3)^2} =-1y(1) = \frac{3*1-4}{2*1-3} =\frac{-1}{-1} =1y_k=1-1(x-1)boldsymbol{y_k= -x+2}    - это уравнение касательной в точке х₀= 1.

И эта прямая ║ прямой у = -x +3

Найдем уравнение касательной в точке  х₀ = 2

Подставим  х₀ в формулу касательной.

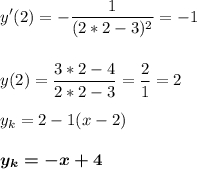\displaystyle y'( 2) = -\frac{1}{(2*2-3)^2} =-1y(2) = \frac{3*2-4}{2*2-3} =\frac{2}{1} =2y_k=2-1(x-2)boldsymbol{y_k= -x+4}- это уравнение касательной в точке х₀= 2.

И эта прямая ║ прямой у = -x +3

Таким образом, кривая 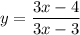   \displaystyle y=\frac{3x-4}{3x-3}   имеет две касательных, параллельных прямой y= -x + 3


Найдите уравнение касательной к кривой y=3x-4/2x-3, параллельных прямой y=-x+3
LinaMat
LinaMat
4,4(77 оценок)
Деление                деление              деление              деление      на 2                      на 5                    на 10                    на 3     772                      775                        770                      771   8766                    8765                    8760                    8763   3002                    3005                    3000                  3003     242                      245                        240                    243     614                      615                        610                      612

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS