29.01.2023 13:29

Есть ответ 👍

В равнобедренном треугольнике со сторонами 8 см, 8 см и 12 см через вершины углов при основании проведены прямые параллельно боковым сторонам. Найдите расстояние от точки пересечения этих прямых до основания треугольника. Cavablardan birini seçin: A. 6 см B. 4/3 см с. 2√/7 см D. 14 CM E.3√5 см

233

366

Посмотреть ответы 3

Ответы на вопрос:

dff45rt96

Математика

4,4(63 оценок)

Пошаговое объяснение:

нам дан треугольник АВС, АВ=ВС=8 см

есть два варианта прямых проведенных через вершины углов при основании, это пара АВ и ВС, либо AD и DC

на решение это не повлияет, так как из-за их параллельности, мы получаем AD=DC=AB=BC=8

тогда чтобы найти расстояние от точки пересечения одной из пар, надо найти высоту треугольника

найдем ОВ по теореме Пифагора:

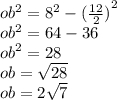
$ob {}^{2} = {8}^{2} - {( \frac{12}{2}) }^{2} \\ ob {}^{2} = 64 - 36 \\ {ob}^{2} = 28 \\ ob = \sqrt{28} \\ ob = 2 \sqrt{7}$

следовательно ответ 2√7

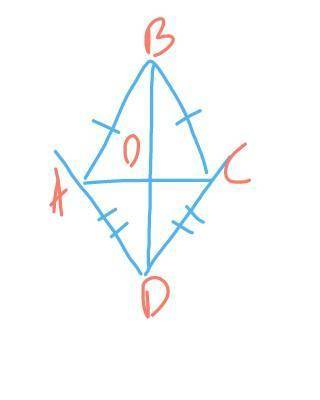
В равнобедренном треугольнике со сторонами 8 см, 8 см и 12 см через вершины углов при основании пров

никуся1984

Математика

4,5(48 оценок)

2√7 см

Объяснение:

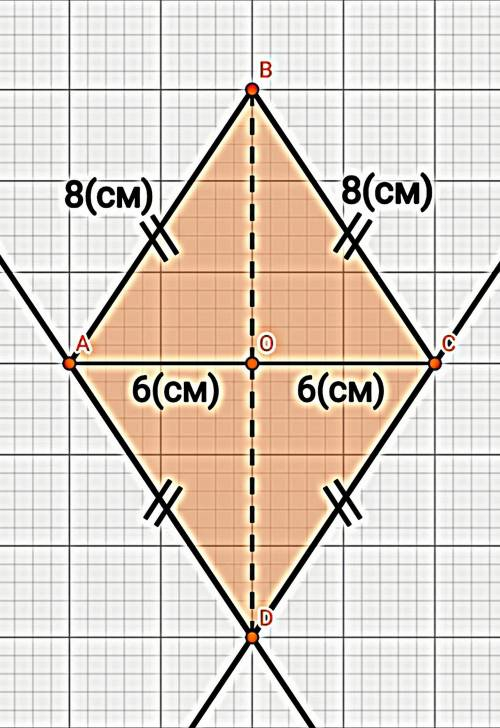
Дано: пусть ∆АВС, АВ = ВС = 8см, АС = 12см

Найти: DO - ?

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение Это ромб. Стороны попарно параллельны и диагонали перпендикулярны и точкой пересечения делятся пополам. DО=ОВ. AO=OC=6см∆АВО - прямоугольный. Найдем Катет (ВО) применив теорему Пифагора. Она гласит, что квадрат гипотенузы равен сумме квадратов катетов.

⠀⠀⠀⠀AB²=BO² + AO²

⠀⠀⠀⠀8² = ВО² + 6²

Отсюда выразим катет ВО.

⠀⠀⠀⠀ВО² = 8² - 6²

⠀⠀⠀⠀ВО² = 64 - 36

⠀⠀⠀⠀ВО² = 28

Извлечем корень.

⠀⠀⠀⠀ВО = √28

⠀⠀⠀⠀ВО = 2√7(см)

Т.к. ВО = DO, то ответ 2√7(см)
В равнобедренном треугольнике со сторонами 8 см, 8 см и 12 см через вершины углов при основании пров

saksharovsasha

Математика

4,4(91 оценок)

100кг., 500кг., 700кг., 200кг., 900кг., 300кг.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.