Регистрация Спросить otvet5GPT
красотка248
05.07.2022 11:06
Алгебра
Есть ответ 👍

Порівняйте значення тригонометричних функцій 1) sin() і sin()
2) cos() і cos()

141
158
Посмотреть ответы 2

Ответы на вопрос:

ariana201723
ariana201723
4,5(39 оценок)

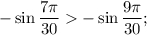
1) - \sin \displaystyle\frac{{7\pi }}{{30}} - \sin \displaystyle\frac{{9\pi }}{{30}};

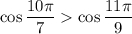
2) \cos \displaystyle\frac{{10\pi }}{7} \cos \displaystyle\frac{{11\pi }}{9}

Объяснение:

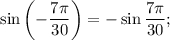
1) \sin \left( { - \displaystyle\frac{{7\pi }}{{30}}} \right) = - \sin \displaystyle\frac{{7\pi }}{{30}};

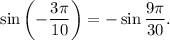
\sin \left( { - \displaystyle\frac{{3\pi }}{{10}}} \right) = - \sin \displaystyle\frac{{9\pi }}{{30}}.

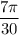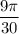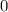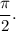Оба аргумента \displaystyle\frac{{7\pi }}{{30}} и \displaystyle\frac{{9\pi }}{{30}} принадлежат промежутку от 0 до \displaystyle\frac{\pi }{2}. В этом промежутке функция 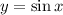y = \sin x возрастает. Это значит, что чем больше значение аргумента, тем больше значение функции. Отсюда

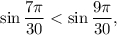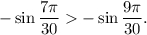
\sin \displaystyle\frac{{7\pi }}{{30}} < \sin \displaystyle\frac{{9\pi }}{{30}}, тогда - \sin \displaystyle\frac{{7\pi }}{{30}} - \sin \displaystyle\frac{{9\pi }}{{30}}.

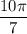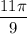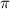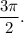2) Оба аргумента \displaystyle\frac{{10\pi }}{7} и \displaystyle\frac{{11\pi }}{9} принадлежат промежутку от \pi  до \displaystyle\frac{{3\pi }}{2}. В этом промежутке функция 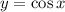y = \cos x возрастает. Это означает, что чем больше значение аргумента, тем больше значение функции. Отсюда

\cos \displaystyle\frac{{10\pi }}{7} = \cos \displaystyle\frac{{90\pi }}{{63}} \cos \displaystyle\frac{{77\pi }}{{63}} = \cos \displaystyle\frac{{11\pi }}{9}.

kazan20001202
kazan20001202
4,4(24 оценок)
1.z*(9-z)=i z=o 9-z=o z=i z=9 -2x^2-4x=o x^2+2x=o x^2+2x+1=1 (x+1)^2=1 x=-2 x=0 1-z^2=0 -z^2==-1 z=-1 z=1 3z^2-75=0 z^=25 z=5 7-2x/2x * 5x-8/8x=0 x=7/2 x неравно 0 x=8/5 x=1,6 3x+8/4x * 4x-12/3x =0 3x+8/4x=0 4x-12/3=0 x=-8/3 x=3

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS