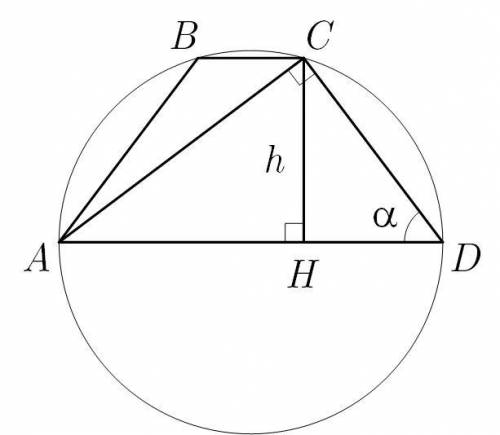
Диагональ равносторонней трапеции перпендикулярна боковой стороне, а угол между боковой стороной и большим основанием трапеции равен . Найдите радиус окружности, описанной вокруг
трапеции, если ее высота равна h.

176

195

Посмотреть ответы 2

Ответы на вопрос:

davlud1974

Геометрия

4,7(28 оценок)

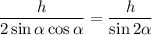
$\displaystyle\frac{h}{{2\sin \alpha \cos \alpha }}=\displaystyle\frac{h}{{\sin 2\alpha }}$

Объяснение:

Используя метрические соотношения в прямоугольном треугольнике из треугольника 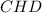CHD получаем:

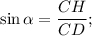
$\sin \alpha = \displaystyle\frac{{CH}}{{CD}};$

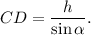
$CD = \displaystyle\frac{h}{{\sin \alpha }}.$

Тогда из треугольника 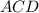ACD

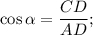
$\cos \alpha = \displaystyle\frac{{CD}}{{AD}};$

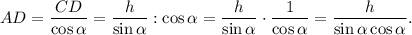
$AD = \displaystyle\frac{{CD}}{{\cos \alpha }} = \displaystyle\frac{h}{{\sin \alpha }}:\cos \alpha = \displaystyle\frac{h}{{\sin \alpha }} \cdot \displaystyle\frac{1}{{\cos \alpha }} = \displaystyle\frac{h}{{\sin \alpha \cos \alpha }}.$

Описанная окружность трапеции одновременно является описанной окружностью вокруг прямоугольного треугольника 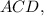ACD, значит ее радиус равен половине гипотенузы:

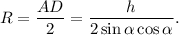
$R = \displaystyle\frac{{AD}}{2} = \displaystyle\frac{h}{{2\sin \alpha \cos \alpha }}.$

Пользуясь знаниями по тригонометрии 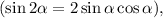$(\sin 2\alpha = 2\sin \alpha \cos \alpha ),$ можно записать ответ компактнее:

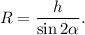
$R = \displaystyle\frac{h}{{\sin 2\alpha }}.$

Диагональ равносторонней трапеции перпендикулярна боковой стороне, а угол между боковой стороной и б

tekkenknigin

Геометрия

4,6(91 оценок)

По формуле: 1+tg^2a=1/cos^2a

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.