Регистрация Спросить otvet5GPT
ellalavrina
04.02.2022 20:00
Алгебра
Есть ответ 👍

Найти абсциссу точки, в которой касательная к графику функции f(x)=2√x +x параллельна прямой y=2x

236
287
Посмотреть ответы 2

Ответы на вопрос:

нурбол5
нурбол5
4,4(34 оценок)

абсциссf   точки   х₀ = 1

Объяснение:

Прежде всего найдем уравнение касательной.

Уравнение касательной имеет вид

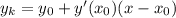
y_k = y_0 + y'(x_0)(x - x_0)

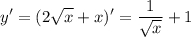
\displaystyle y'=(2\sqrt{x} +x )'=\frac{1}{\sqrt{x} } +1

Рассмотрим уравнение касательной  в точке х₀ (эту точку нам и надо найти)

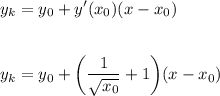
\displaystyle y_k = y_0 + y'(x_0)(x - x_0)y_k = y_0 + \bigg(\frac{1}{\sqrt{x_0} } +1\bigg)(x - x_0)

Для того, чтобы две прямые были параллельны, необходимо,  чтобы в уравнениях прямых коэффициенты при х были бы равны.

У прямой у = 2х  коэффициент при х равен 2

У касательной коэффициент при х равен 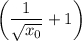  \displaystyle \bigg(\frac{1}{\sqrt{x_0} } +1\bigg)

Приравняем коэффициенты и найдем х₀

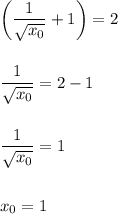
\displaystyle \bigg(\frac{1}{\sqrt{x_0} } +1\bigg)=2displaystyle \frac{1}{\sqrt{x_0} } =2-1frac{1}{\sqrt{x_0} } =1x_0=1

Проверим.

Подставим  х₀ в формулу касательной.

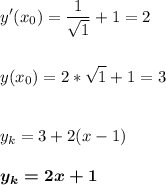\displaystyle y'( x_0) = \frac{1}{\sqrt{1} } +1=2y(x_0)=2*\sqrt{1} +1 = 3y_k = 3+2(x-1)boldsymbol { y_k = 2x+1}- это уравнение касательной в точке х₀=1.

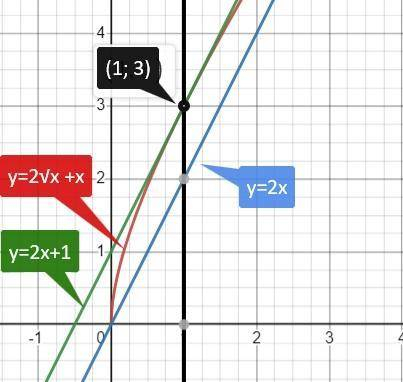
И эта прямая ║ прямой у = 2х  


Найти абсциссу точки, в которой касательная к графику функции f(x)=2√x +x параллельна прямой y=2x
VIP161
VIP161
4,4(76 оценок)

треба робити оцінкою

-1< sinx< 1

0< sin^2x< 1

-3< sin^2x-3< -2

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS