25.03.2023 09:55

Есть ответ 👍

с заданием по высшей математике Задание 9,10
Чертить кривые не нужно

Дана кривая x^2 + 4y = 0. Докажите, что данная кривая — парабола. Найдите координаты её вершины. Найдите значение её параметра p. Запишите уравнение её оси симметрии.

Дана кривая 5x^2 + 8y^2 + 4xy − 24x − 24y = 0. Докажите, что эта кривая — эллипс. Найдите координаты центра его симметрии. Найдите его большую и малую полуоси. Запишите уравнение фокальной оси.

114

146

Посмотреть ответы 2

Ответы на вопрос:

molokomo

Математика

4,5(65 оценок)

9.2. (0, 0)

9.3. p = 2

9.4. x = 0

10.2. (2, 1)

10.3. a = 2, b = 3

10.4. x + 2y - 4 = 0

Пояснение:

9.1. Каноническое уравнение параболы можно записать в виде 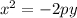x^2=-2py . В нашем случае 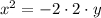$x^2=-2\cdot 2\cdot y$ , что соответствует этому уравнению.

9.2. Поскольку уравнение соответствует каноническому, преобразования координат не произошло. Значит, вершина параболы находится в точке (0, 0).

9.3. Из п. 9.1 p = 2.

9.4. Если точка (x, y) принадлежит параболе, то и точка (-x, y) принадлежит ей (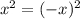 x^2=(-x)^2 ), значит, её ось симметрии — прямая x = 0.

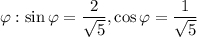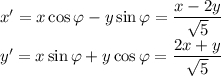10.1. Выполним поворот на угол $\varphi:\sin{\varphi}=\dfrac{2}{\sqrt{5}},\cos{\varphi}=\dfrac{1}{\sqrt{5}}$ . Воспользуемся формулами $x'=x\cos{\varphi}-y\sin{\varphi}=\dfrac{x-2y}{\sqrt{5}}\\y'=x\sin{\varphi}+y\cos{\varphi}=\dfrac{2x+y}{\sqrt{5}}$ :

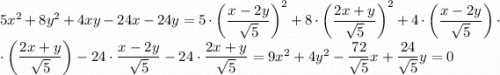
$5x^2+8y^2+4xy-24x-24y=5\cdot\left(\dfrac{x-2y}{\sqrt{5}}\right)^2+8\cdot\left(\dfrac{2x+y}{\sqrt{5}}\right)^2+4\cdot\left(\dfrac{x-2y}{\sqrt{5}}\right)\cdot\\\cdot\left(\dfrac{2x+y}{\sqrt{5}}\right)-24\cdot\dfrac{x-2y}{\sqrt{5}}-24\cdot\dfrac{2x+y}{\sqrt{5}}=9x^2+4y^2-\dfrac{72}{\sqrt{5}}x+\dfrac{24}{\sqrt{5}}y=0$

Выполним параллельный перенос начала координат на вектор 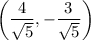$\left(\dfrac{4}{\sqrt{5}},-\dfrac{3}{\sqrt{5}}\right)$ . Воспользуемся формулами 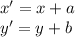$x'=x+a\\y'=y+b$ (a, b — координаты вектора):

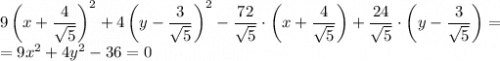
$9\left(x+\dfrac{4}{\sqrt{5}}\right)^2+4\left(y-\dfrac{3}{\sqrt{5}}\right)^2-\dfrac{72}{\sqrt{5}}\cdot\left(x+\dfrac{4}{\sqrt{5}}\right)+\dfrac{24}{\sqrt{5}}\cdot\left(y-\dfrac{3}{\sqrt{5}}\right)=\\=9x^2+4y^2-36=0$

Поделим обе части уравнения на 36:

$9x^2+4y^2=36\\\dfrac{x^2}{4}+\dfrac{y^2}{9}=1$

Получили каноническое уравнение эллипса.

10.2. В полученном в п. 10.1 уравнении центр симметрии находится в точке (0, 0). Чтобы получить центр симметрии исходного эллипса, необходимо провести преобразования координат в обратном порядке (поскольку действия проводились над системой координат, а теперь — над точкой, то формулы останутся такими же):

параллельный перенос: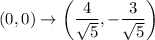 $(0,0)\rightarrow\left(\dfrac{4}{\sqrt{5}},-\dfrac{3}{\sqrt{5}}\right)$ поворот: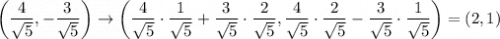 $\left(\dfrac{4}{\sqrt{5}},-\dfrac{3}{\sqrt{5}}\right)\rightarrow\left(\dfrac{4}{\sqrt{5}}\cdot\dfrac{1}{\sqrt{5}}+\dfrac{3}{\sqrt{5}}\cdot\dfrac{2}{\sqrt{5}},\dfrac{4}{\sqrt{5}}\cdot\dfrac{2}{\sqrt{5}}-\dfrac{3}{\sqrt{5}}\cdot\dfrac{1}{\sqrt{5}}\right)=(2,1)$

10.3. Из уравнения, полученного в п. 10.1: большая полуось b = 3, малая полуось a = 2.

10.4. Уравнение фокальной оси в полученном уравнении: x = 0. Выполним преобразования координат в обратном порядке:

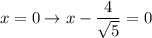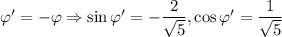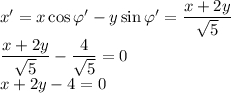
параллельный перенос: $x=0\rightarrow x-\dfrac{4}{\sqrt{5}}=0$ поворот (на угол $\varphi'=-\varphi\Rightarrow\sin{\varphi'}=-\dfrac{2}{\sqrt{5}},\cos{\varphi'}=\dfrac{1}{\sqrt{5}}$ ): $x'=x\cos{\varphi'}-y\sin{\varphi'}=\dfrac{x+2y}{\sqrt{5}}\\\dfrac{x+2y}{\sqrt{5}}-\dfrac{4}{\sqrt{5}}=0\\x+2y-4=0$

PolinaGetto

Математика

4,7(8 оценок)

Поставил бы таблички, указывающие на то, что стирать одежду в озере, мыть машину у озера и выливать отходы с мусором нельзя. нужна вода - набери ее в ведро

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.