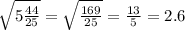Регистрация Спросить otvet5GPT
slava202011
10.02.2023 06:50
Алгебра
Есть ответ 👍

Доказать тригонометрическое тождество

202
460
Посмотреть ответы 2

Ответы на вопрос:

annaoroku3
annaoroku3
4,8(57 оценок)

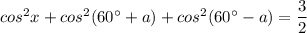
          cos^2x+cos^2(60^\circ +a)+cos^2(60^\circ-a)=\dfrac{3}{2}

Применяем формулу понижения степени 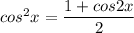  cos^2x=\dfrac{1+cos2x}{2}   ,

формулу суммы косинусов , а также формулы приведения .

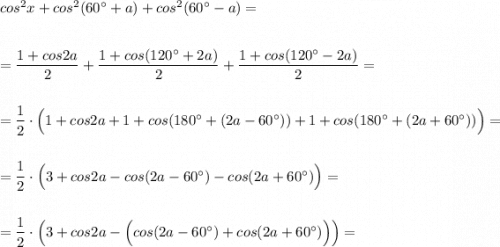
cos^2x+cos^2(60^\circ +a)+cos^2(60^\circ-a)==\dfrac{1+cos2a}{2}+\dfrac{1+cos(120^\circ +2a)}{2}+\dfrac{1+cos(120^\circ -2a)}{2}==\dfrac{1}{2}\cdot \Big(1+cos2a+1+cos(180^\circ +(2a-60^\circ))+1+cos(180^\circ+(2a+60^\circ ))\Big)==\dfrac{1}{2}\cdot \Big(3+cos2a-cos(2a-60^\circ)-cos(2a+60^\circ )\Big)==\dfrac{1}{2}\cdot \Big(3+cos2a-\Big(cos(2a-60^\circ)+cos(2a+60^\circ )\Big)\Big)=  

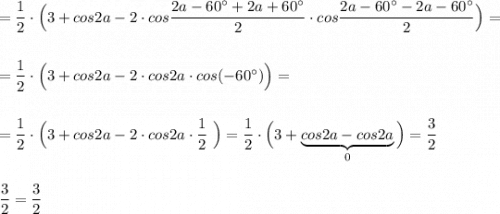
=\dfrac{1}{2}\cdot \Big(3+cos2a-2\cdot cos\dfrac{2a-60^\circ +2a+60^\circ }{2}\cdot cos\dfrac{2a-60^\circ -2a-60^\circ }{2}\Big)==\dfrac{1}{2}\cdot \Big(3+cos2a-2\cdot cos2a\cdot cos(-60^\circ )\Big)==\dfrac{1}{2}\cdot \Big(3+cos2a-2\cdot cos2a\cdot \dfrac{1}{2}\ \Big)=\dfrac{1}{2}\cdot \Big(3+\underbrace{cos2a-cos2a}_{0}\Big)=\dfrac{3}{2}dfrac{3}{2}=\dfrac{3}{2}  

Тождество доказано .

Bert18
Bert18
4,5(72 оценок)

\sqrt{5\frac{44}{25} } =\sqrt{\frac{169}{25} } =\frac{13}{5} =2.6

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS