Регистрация Спросить otvet5GPT
Raha0056
17.10.2021 06:25
Алгебра
Есть ответ 👍

Решиет уравнение :
x^2 + y^2 = 4
x^3 + y^3 = -8

221
368
Посмотреть ответы 2

Ответы на вопрос:

karrtavaya01
karrtavaya01
4,6(82 оценок)

(0; –2), (–2; 0)

Объяснение:

Пускай 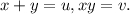x + y = u, xy = v. Тогда

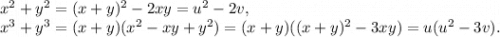
{x^2} + {y^2} = {(x + y)^2} - 2xy = {u^2} - 2v,\\{x^3} + {y^3} = (x + y)({x^2} - xy + {y^2}) = (x + y)({(x + y)^2} - 3xy) = u({u^2} - 3v).

Данная система перепишется в виде

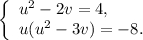
\left\{ \begin{array}{l}{u^2} - 2v = 4,\\u({u^2} - 3v) = - 8.\end{array} \right.

Из первого уравнения 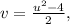v = \frac{{{u^2} - 4}}{2}, тогда

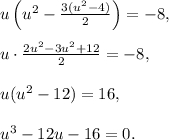
u\left( {{u^2} - \frac{{3({u^2} - 4)}}{2}} \right) = - 8, u \cdot \frac{{2{u^2} - 3{u^2} + 12}}{2} = - 8,\\ \\u({u^2} - 12) = 16, {u^3} - 12u - 16 = 0.

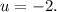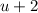По теореме Безу ищем целые корни такого уравнения среди делителей свободного члена, находим подходящее значение u = - 2. Выполняя деление многочлена {u^3} - 12u - 16 на u + 2 в столбик, получаем: 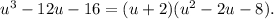{u^3} - 12u - 16 = (u + 2)({u^2} - 2u - 8). Квадратный трехчлен 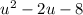{u^2} - 2u - 8 имеет корни –2 и 4.

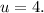Таким образом, u = - 2 или u = 4. Им соответствуют 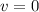v = 0 или v = 6.

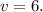
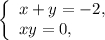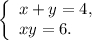Делая обратную замену, получаем две системы: \left\{ \begin{array}{l}x + y = - 2,\\xy = 0,\end{array} \right. и \left\{ \begin{array}{l}x + y = 4,\\xy = 6.\end{array} \right. С теоремы, обратной теореме Виета, находим пары решений первой системы: (0; –2), (–2; 0). Вторая система решений не имеет.

Лолита171107
Лолита171107
4,4(88 оценок)

Відповідь:2а-10>а^2-10а; -а^2+12а-10=0;D=. Далі знайдіть самі, бо дискримінант і корені дискримінанта - легко

Пояснення:

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS