Регистрация Спросить otvet5GPT
Miras19932708
01.02.2023 08:59
Математика
Есть ответ 👍

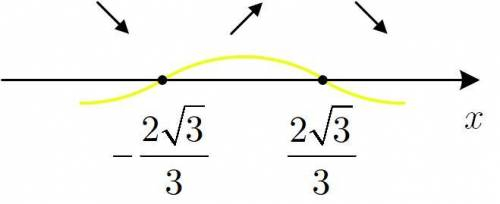
Найдите высоту цилиндра наибольшего объема, который можно вписать в шар радиуса 1.

181
216
Посмотреть ответы 2

Ответы на вопрос:

gels5344Inetka
gels5344Inetka
4,6(95 оценок)

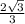
\frac{{2\sqrt 3 }}{3}

Пошаговое объяснение:

Рассмотрим осевое сечение. По условию 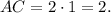AC = 2 \cdot 1 = 2. Пусть высота цилиндра 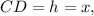CD = h = x, тогда из прямоугольного треугольника 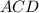ACD по теореме Пифагора 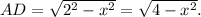AD = \sqrt {{2^2} - {x^2}} = \sqrt {4 - {x^2}} . Отсюда радиус основания цилиндра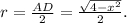 r = \frac{{AD}}{2} = \frac{{\sqrt {4 - {x^2}} }}{2}.

Объем цилиндра 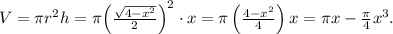V = \pi {r^2}h = \pi {\left( {\frac{{\sqrt {4 - {x^2}} }}{2}} \right)^2} \cdot x = \pi \left( {\frac{{4 - {x^2}}}{4}} \right)x = \pi x - \frac{\pi }{4}{x^3}.

Найдем производную от объема пользуясь дважды формулой 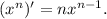({x^n})' = n{x^{n - 1}}.

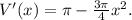
V'(x) = \pi - \frac{{3\pi }}{4}{x^2}.

Уравнение 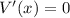V'(x) = 0 имеет корни 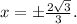x = \pm \frac{{2\sqrt 3 }}{3}. С метода интервалов убеждаемся, что точка 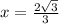x = \frac{{2\sqrt 3 }}{3} является точкой максимума функции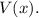 V(x).


Найдите высоту цилиндра наибольшего объема, который можно вписать в шар радиуса 1.
Найдите высоту цилиндра наибольшего объема, который можно вписать в шар радиуса 1.
Darya789
Darya789
4,7(95 оценок)
Первое действие выполняется в скобках 20: (63/14+111//4-23/4): 5= 1.63/14=4.5 2.111/14=7.93 20: (4.5+7./4-23/4): 5=(20: 12./4-23/4): 5 1.41/4=10.25 2.23/4=5.75 (20: 12..25-5.75): 5 1.20: 12.43=1.6 2.10.25-5.75=4.5 1.6-(4.5: 5)=1.6-0.9=0.7 4.5/5=0.9

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS