Алгебра: Данная функция такая что для любого Найдите

Шишкин555

05.03.2023 03:11

Алгебра

Есть ответ 👍

Данная функция такая что для любого
Найдите

128

400

Посмотреть ответы 2

Ответы на вопрос:

Сербина

Алгебра

4,4(99 оценок)

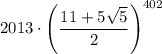
$2013\cdot\left(\dfrac{11+5\sqrt{5}}{2}\right)^{402}$

Объяснение:

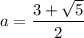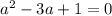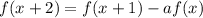Заметим, что число $a=\dfrac{3+\sqrt{5}}{2}$ является корнем квадратного уравнения a^2-3a+1=0 . Распишем f(2013), используя соотношение f(x+2)=f(x+1)-af(x) :

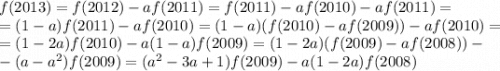
$f(2013)=f(2012)-af(2011)=f(2011)-af(2010)-af(2011)=\\=(1-a)f(2011)-af(2010)=(1-a)(f(2010)-af(2009))-af(2010)=\\=(1-2a)f(2010)-a(1-a)f(2009)=(1-2a)(f(2009)-af(2008))-\\-(a-a^2)f(2009)=(a^2-3a+1)f(2009)-a(1-2a)f(2008)$

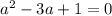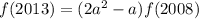Поскольку a^2-3a+1=0 , то f(2013)=(2a^2-a)f(2008) .

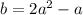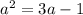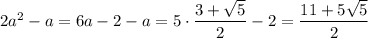Вычислим значение выражения b=2a^2-a , также используя, что a^2=3a-1 : $2a^2-a=6a-2-a=5\cdot\dfrac{3+\sqrt{5}}{2}-2=\dfrac{11+5\sqrt{5}}{2}$ .

Таким образом, для функции получили следующее рекуррентное соотношение: 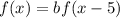f(x)=bf(x-5) . Его можно продолжить следующим образом:

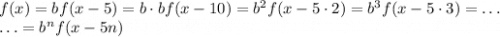
$f(x)=bf(x-5)=b\cdot bf(x-10)=b^2f(x-5\cdot 2)=b^3f(x-5\cdot 3)=\ldots\\ \ldots =b^nf(x-5n)$

Тогда 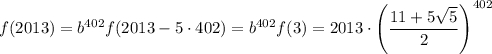$f(2013)=b^{402}f(2013-5\cdot 402)=b^{402}f(3)=2013\cdot\left(\dfrac{11+5\sqrt{5}}{2}\right)^{402}$ .

mimimi055

Алгебра

4,5(27 оценок)

АА1 - биссектриса ⇒ ∠САА1=∠ВАА1=55° , ∠А=2*55°=110°

ВВ1 - биссектриса ⇒ ∠СВВ1=∠АВВ1=23° , ∠В=2*23°=46°

∠С=180°-(110°+46°)=24°

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.