Регистрация Спросить otvet5GPT
Mussa1
14.04.2020 19:19
Математика
Есть ответ 👍

Найти производные y' =dy/dx заданных функций

238
267
Посмотреть ответы 2

Ответы на вопрос:

36kot361
36kot361
4,7(14 оценок)

Пошаговое объяснение:

б) \[{\mathop{\rm tg}\nolimits} y = xy + \ln xy;\]

Подразумеваем, что 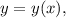y = y(x), дифференцируем обе части по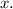 x.

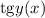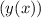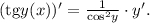
Так, {\mathop{\rm tg}\nolimits} y(x) — сложная функция, поэтому ее производная это сперва производная от тангенса, умноженная на производную от его аргумента (y(x)): ({\mathop{\rm tg}\nolimits} y(x))' = \frac{1}\cos }^2}y}} \cdot y'.

Находим производную xy как производную произведения: 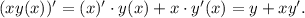(xy(x))' = (x)' \cdot y(x) + x \cdot y'(x) = y + xy'.

Производная логарифма — опять сложная функция: 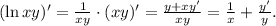(\ln xy)' = \frac{1}{{xy}} \cdot (xy)' = \frac{{y + xy'}}{{xy}} = \frac{1}{x} + \frac{{y'}}{y}.

Вместе получаем: 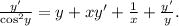\frac{{y'}}\cos }^2}y}} = y + xy' + \frac{1}{x} + \frac{{y'}}{y}.

Выражаем 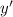y' из последнего равенства. Можно преобразовать ответ, избавившись от «двухэтажных» дробей: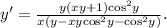 y' = \frac{{y(xy + 1){{\cos }^2}y}}{{x(y - xy{{\cos }^2}y - {{\cos }^2}y)}}.

в) 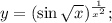y = {(\sin \sqrt x )^{\frac{1}{{{x^2;

Прологарифмируем по натуральному основанию обе части данного равенства: 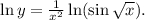\ln y = \frac{1}{{{x^2}}}\ln (\sin \sqrt x ). Теперь найдем производную от обеих частей аналогично решению п. б).

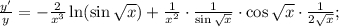
\frac{{y'}}{y} = - \frac{2}{{{x^3}}}\ln (\sin \sqrt x ) + \frac{1}{{{x^2}}} \cdot \frac{1}{{\sin \sqrt x }} \cdot \cos \sqrt x \cdot \frac{1}{{2\sqrt x }};\\

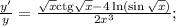
\frac{{y'}}{y} = \frac{{\sqrt x {\mathop{\rm ctg}\nolimits} \sqrt x - 4\ln (\sin \sqrt x )}}{{2{x^3}}};\\

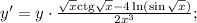
y' = y \cdot \frac{{\sqrt x {\mathop{\rm ctg}\nolimits} \sqrt x - 4\ln (\sin \sqrt x )}}{{2{x^3}}};\\

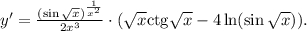
y' = \frac(\sin \sqrt x )}^{\frac{1}{{{x^2{{2{x^3}}} \cdot (\sqrt x {\mathop{\rm ctg}\nolimits} \sqrt x - 4\ln (\sin \sqrt x )).\\

etomalo
etomalo
4,6(30 оценок)
22х -10 -17х=55, 22х-17х=55+10, 5х = 65, х=13. 2(11(13) -5) - 17(13)=55, 55=55. 2) 40х +15 -12=83, 40х= 83-15+12, 40х=80, х=2. 5(8(2) +3) -12=83, 83=83

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS