Математика: с тригонометрическим уравнением

Mary090605

04.05.2023 21:15

Математика

Есть ответ 👍

с тригонометрическим уравнением

155

458

Посмотреть ответы 2

Ответы на вопрос:

элизабет35

Математика

4,8(45 оценок)

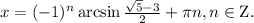
$x = {( - 1)^n}\arcsin \frac{{\sqrt 5 - 3}}{2} + \pi n, n\in {\rm Z}.$

Пошаговое объяснение:

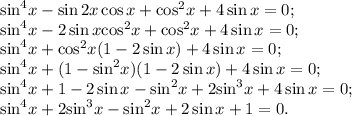
${\sin ^4}x - \sin 2x\cos x + {\cos ^2}x + 4\sin x = 0;\\{\sin ^4}x - 2\sin x{\cos ^2}x + {\cos ^2}x + 4\sin x = 0;\\{\sin ^4}x + {\cos ^2}x(1 - 2\sin x) + 4\sin x = 0;\\{\sin ^4}x + (1 - {\sin ^2}x)(1 - 2\sin x) + 4\sin x = 0;\\{\sin ^4}x + 1 - 2\sin x - {\sin ^2}x + 2{\sin ^3}x + 4\sin x = 0;\\{\sin ^4}x + 2{\sin ^3}x - {\sin ^2}x + 2\sin x + 1 = 0.$

Поделим полученное уравнение на 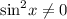${\sin ^2}x \ne 0$ :

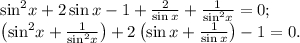
${\sin ^2}x + 2\sin x - 1 + \frac{2}{{\sin x}} + \frac{1}\sin }^2}x}} = 0;\\\left( {{{\sin }^2}x + \frac{1}\sin }^2}x}}} \right) + 2\left( {\sin x + \frac{1}{{\sin x}}} \right) - 1 = 0.$

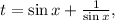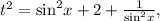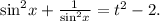
Сделаем замену $t = \sin x + \frac{1}{{\sin x}},$ тогда ${t^2} = {\sin ^2}x + 2 + \frac{1}\sin }^2}x}},$ откуда ${\sin ^2}x + \frac{1}\sin }^2}x}} = {t^2} - 2.$

Заметим, что 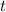как сумма двух взаимно обратных величин всегда по модулю не меньше 2.

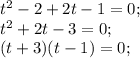
${t^2} - 2 + 2t - 1 = 0;\\{t^2} + 2t - 3 = 0;\\(t + 3)(t - 1) = 0;$

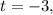
t = - 3, t = 1 (посторонний корень).

Делаем обратную замену:

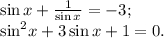
$\sin x + \frac{1}{{\sin x}} = - 3;\\{\sin ^2}x + 3\sin x + 1 = 0.$

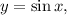
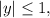
Делаем замену $y = \sin x,$ $\left| y \right| \le 1,$ ${y^2} + 3y + 1 = 0.$

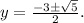
Дискриминант последнего квадратного уравнения D = 9 - 4 = 5, корни $y = \frac{{ - 3 \pm \sqrt 5 }}{2}.$

Значение 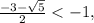$\frac{{ - 3 - \sqrt 5 }}{2} < - 1,$ поэтому 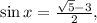$\sin x = \frac{{\sqrt 5 - 3}}{2},$ откуда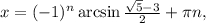 $x = {( - 1)^n}\arcsin \frac{{\sqrt 5 - 3}}{2} + \pi n,$ $n\in {\rm Z}.$

neumnaya4044

Математика

4,7(32 оценок)

1)<

2= 3< 4> 5> 6= 7< 8> 9>.............

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.