Ответы на вопрос:
![a \in \left[ {\frac{\pi }{2};\,\,\frac{{3\pi }}{2} - 3} \right] \cup \left[ {\frac{{5\pi }}{2} - 6;\,\,\frac{{7\pi }}{2} - 9} \right]](/tpl/images/4978/4058/57fa2.png)
Пошаговое объяснение:
Правая часть уравнения принимает значения 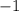 или
или  в зависимости от значений
в зависимости от значений  :
:
при ![2k - 1 \le x < 2k \cos (\pi \cdot [x]) = - 1,](/tpl/images/4978/4058/23d33.png)
при ![2k \le x < 2k + 1 \cos (\pi \cdot [x]) = 1](/tpl/images/4978/4058/92db2.png) для любого целого
для любого целого 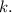
В итоге получается уравнение вида  которое равносильно уравнению
которое равносильно уравнению
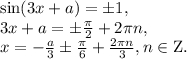
Рассмотрим три промежутка:
1) 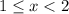
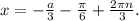
Несложно установить, что только при 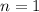 корни такого вида при заданном диапазоне
корни такого вида при заданном диапазоне  попадают в промежуток
попадают в промежуток 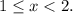 Значит если на этом промежутке уравнение имеет корень, он равен
Значит если на этом промежутке уравнение имеет корень, он равен 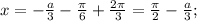
 при
при ![a \in \left[ {0;\,\,\frac{{3\pi }}{2} - 3} \right].](/tpl/images/4978/4058/112c4.png)
2) 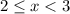
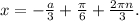
Аналогично, только при 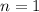 корни такого вида при заданном диапазоне
корни такого вида при заданном диапазоне  попадают в промежуток
попадают в промежуток 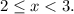 Значит если на этом промежутке уравнение имеет корень, он равен
Значит если на этом промежутке уравнение имеет корень, он равен 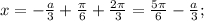
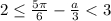 при
при ![a \in \left[ {0;\,\,\frac{{5\pi }}{2} - 6} \right].](/tpl/images/4978/4058/0d30d.png)
3) 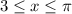
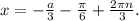
Аналогично, при 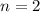 корни такого вида при заданном диапазоне
корни такого вида при заданном диапазоне  попадают в промежуток
попадают в промежуток 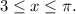 Значит если на этом промежутке уравнение имеет корень, он равен
Значит если на этом промежутке уравнение имеет корень, он равен 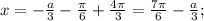
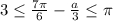 при
при 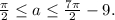
Обозначим на рисунке указанные интервалы. Для существования нечетного количества корней выберем промежутки, на которых пересекаются все три из них или находится только один. Получаем ![a \in \left[ {\frac{\pi }{2};\,\,\frac{{3\pi }}{2} - 3} \right] \cup \left[ {\frac{{5\pi }}{2} - 6;\,\,\frac{{7\pi }}{2} - 9} \right]](/tpl/images/4978/4058/57fa2.png) .
.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Акула в длину может достигать 20 м кит может быть на 13 м длиннее,...
 Anastasiya210815.10.2020 16:48
Anastasiya210815.10.2020 16:48 -
Всантиметрах-12 дм, 9 дм 6 см, 1 м 88 см, 130 мм....
 издательство117.03.2021 23:50
издательство117.03.2021 23:50 -
Отец купил сыну костюм за 24р на что израсходовал 1/3 своих денег...
 Raptilla29.03.2020 12:25
Raptilla29.03.2020 12:25 -
2.4 помножити(2,5 а-1,5в)+6,5(1,8в+5,6а) спростить...
 saa2030.01.2021 06:06
saa2030.01.2021 06:06 -
Впервой бригаде неизвестно во второй в 3 раза больше в двух бригадах...
 faraon2115.09.2022 21:09
faraon2115.09.2022 21:09 -
Как продолжить ряд чисел 10,200,3000,...
 Мишутка89012.08.2020 18:31
Мишутка89012.08.2020 18:31 -
За два дні ведмедик посадив 10 дерев. першого дня він посадив...
 kostyan228201.04.2023 22:10
kostyan228201.04.2023 22:10 -
Найди сумму. 236+189+308 (200-30)×5...
 anitabadurova16.09.2022 19:40
anitabadurova16.09.2022 19:40 -
Решите уравнение: х+3х+5=17 3,5х+2.2х=4.56 3.2у-2,7у =0.6 3.7z-z=0.54...
 ОTВЕT04.10.2021 17:55
ОTВЕT04.10.2021 17:55 -
Длина одной стороны прямоугольника 9 см другой на 5 см меньше...
 DOLTONrus15.11.2022 00:37
DOLTONrus15.11.2022 00:37

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
