Регистрация Спросить otvet5GPT
BakerTaka
25.11.2022 10:42
Алгебра
Есть ответ 👍

Найди область определения функции

203
476
Посмотреть ответы 2

Ответы на вопрос:

angelinasestak
angelinasestak
4,4(89 оценок)

3)  Знаменатель дроби не может быть равен 0 .

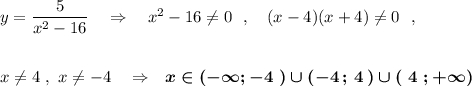
y=\dfrac{5}{x^2-16}\ \ \ \Rightarrow \ \ \ x^2-16\ne 0\ \ ,\ \ \ (x-4)(x+4)\ne 0\ \ ,x\ne 4\ ,\ x\ne -4\ \ \ \Rightarrow \ \ \boldsymbol{x\in (-\infty ;-4\ )\cup (-4\, ;\, 4\, )\cup (\ 4\ ;+\infty )}  

4)  Подкоренное выражение должно быть неотрицательным, а так как корень находится в знаменателе, то ещё и не равным нулю, поэтому

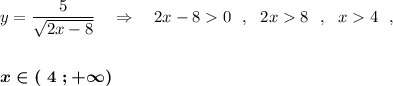
y=\dfrac{5}{\sqrt{2x-8}}\ \ \ \Rightarrow \ \ \ 2x-8 0\ \ ,\ \ 2x 8\ \ ,\ \ x 4\ \ ,boldsymbol{x\in (\ 4\ ;+\infty )}

HAHAEZ2010
HAHAEZ2010
4,7(21 оценок)
Парабола симметричная фигура . это ясно. если сложить ее по оси симметрии, то две ее ветви сольются. то есть сгибать ее надо в точке минимума, так как именно в этой точке она из убывающей становится возрастающей. эта ось симметрии будет параллельна оси оу       . осталось найти координаты точки перегиба.(вершины параболы). для этого есть красивая формула . x0 = - b / 2a. y = 2 x^2 - 5 x + 1; a = 2 ; b = - 5; x0 = 5/4 = 1,25. тогда уравнение оси симметрии примет вид   х = 1,25. другими словами, при любом значении   у   значение х будет равно 1,25. это линия - вертикальная ось  . перпендикулярно оси 0х через точку х =1,25 проводим линию и получаем ось симметрии. 

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS