Регистрация Спросить otvet5GPT
obshaga2311
18.06.2020 16:14
Математика
Есть ответ 👍

Постройте график функций y = корень x .Найдите координаты точек пересечения графика этой функции с прямой x - 2y = 0 (Изобразите графики этих двух функции)

157
404
Посмотреть ответы 3

Ответы на вопрос:

Vasilisa00700
Vasilisa00700
4,6(78 оценок)

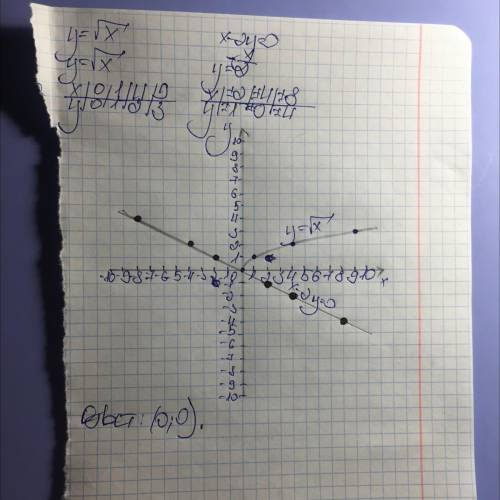
1) Построим график функции у = √х
Мы знаем, что подкоренное выражение всегда больше или равно нулю, т.е. х ≥ 0 из чего следует что и у ≥ 0
Строим график(см. вложение)
2) Построим график функции x-2y = 0
Сначала выразим у из функции
x-2y = 0
2у = х |:2
у = х/2
Строим график(см. вложение)
3) Найдём точки пересечения графиков
Из рисунка видно, что они пересекаются в точках (0;0) и (4;2). Проверим это аналитически
У функций равны левые части ⇒ равны и правые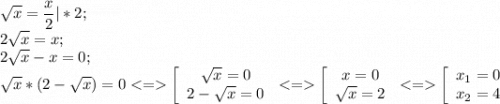
\displaystyle \sqrt{x} =\frac{x}{2}|*2;\\2\sqrt{x} =x;\\2\sqrt{x} -x=0;\\\sqrt{x} *(2-\sqrt{x} )=0 < = \left[\begin{array}{ccc}\sqrt{x} =0\\2-\sqrt{x} =0\\\end{array}\right. < = \left[\begin{array}{ccc}x =0\\\sqrt{x} =2\\\end{array}\right. < = \left[\begin{array}{ccc}x_1 =0\\x_2=4\\\end{array}\right
Теперь подставим значения х в любое выражение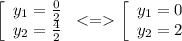
\displaystyle \left[\begin{array}{ccc}y_1 = \frac{0}{2} \\y_2 = \frac{4}{2} \\\end{array}\right. < = \left[\begin{array}{ccc}y_1 = 0\\y_2 = 2\\\end{array}\right.
Получились те же точки (0;0) и (4;2).

Карина2000017
Карина2000017
4,6(26 оценок)
Надеюсь, что (¿)
Постройте график функций y = корень x .Найдите координаты точек пересечения графика этой функции с п
Lord222435
Lord222435
4,7(6 оценок)
Периметр 74 см 1 сторона  25 см 74-(25*2)=24 24/2=12 см =1дм2см

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS