14.10.2021 04:12

Есть ответ 👍

решить систему

при решении иррацтонального неравенства использовать такие равносильные претворения

система +система + объединение систем

167

262

Посмотреть ответы 2

Ответы на вопрос:

Tomi1234

Алгебра

4,7(6 оценок)

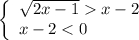
$\left\{\begin{array}{l}\sqrt{2x-1} x-2\\x-2 < 0\end{array}\right$

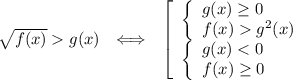
Решаем первое неравенство системы по правилу:

$\sqrt{f(x)} g(x)\ \ \Longleftrightarrow \ \ \left[\begin{array}{l}\left\{\begin{array}{l}g(x)\geq 0\\f(x) g^2(x)\\\end{array}\right\\\left\{\begin{array}{l}g(x) < 0\\f(x)\geq 0\end{array}\right\end{array}\right\end{array}\right$

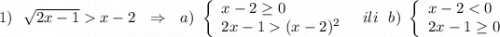
$1)\ \ \sqrt{2x-1} x-2\ \ \Rightarrow \ \ a)\ \left\{\begin{array}{l}x-2\geq 0\\2x-1 (x-2)^2\end{array}\right\ \ ili\ \ b)\ \left\{\begin{array}{l}x-2 < 0\\2x-1\geq 0\end{array}\right$

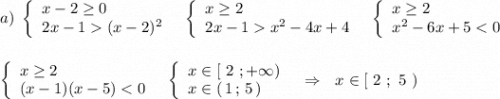
$a)\ \left\{\begin{array}{l}x-2\geq 0\\2x-1 (x-2)^2\end{array}\right\ \ \left\{\begin{array}{l}x\geq 2\\2x-1 x^2-4x+4\end{array}\right\ \ \left\{\begin{array}{l}x\geq 2\\x^2-6x+5 < 0\end{array}\rightleft\{\begin{array}{l}x\geq 2\\(x-1)(x-5) < 0\end{array}\right\ \ \left\{\begin{array}{l}x\in [\ 2\ ;+\infty )\\x\in (\, 1\, ;\, 5\, )\end{array}\right\ \ \Rightarrow \ \ x\in [\ 2\ ;\ 5\ )$

Квадратное неравенство решали методом интервалов:

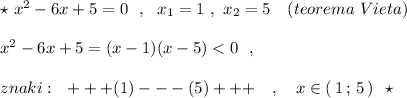
$\star \ x^2-6x+5=0\ \ ,\ \ x_1=1\ ,\ x_2=5\ \ \ (teorema\ Vieta)x^2-6x+5=(x-1)(x-5) < 0\ \ ,znaki:\ \ +++(1)---(5)+++\ \ \ ,\ \ \ x\in (\, 1\, ;\, 5\, )\ \ \star$

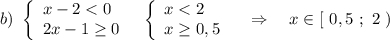
$b)\ \left\{\begin{array}{l}x-2 < 0\\2x-1\geq 0\end{array}\right\ \ \left\{\begin{array}{l}x < 2\\x\geq 0,5\end{array}\right\ \ \ \Rightarrow \ \ \ x\in [\ 0,5\ ;\ 2\ )$

Теперь объединим решения 1 и 2 систем , получим решение 1) иррационального неравенства заданной системы .

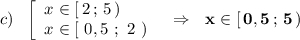
$c)\ \ \left[\begin{array}{l}x\in [\, 2\, ;\, 5\, )\\x\in[\ 0,5\ ;\ 2\ )\end{array}\right\ \ \Rightarrow \ \ \bf x\in [\, 0,5\, ;\, 5\, )$

Итак, 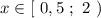$x\in [\ 0,5\ ;\ 2\ )$ - это решение первого неравенства заданной системы.

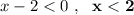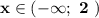2) Решаем второе неравенство заданной системы: $x-2 < 0\ ,\ \ \bf x < 2$ , $\bf x\in (-\infty ;\ 2\ )$ .

3) Теперь найдём решение заданной системы как пересечение решений 1-го и 2-го неравенств заданной системы .

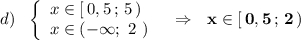
$d)\ \ \left\{\begin{array}{l}x\in [\, 0,5\, ;\, 5\, )\\x\in (-\infty ;\ 2\ )\end{array}\right\ \ \Rightarrow \ \ \bf x\in [\, 0,5\, ;\, 2\, )$

ответ: 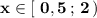$\bf x\in [\ 0,5\, ;\, 2\, )$ .

Можно отметить, что все эти процедуры выполнять не обязательно, так как в условии системы уже задано, что х-2<0 , а (х-2) - это правая часть 1-го неравенства. То есть специально рассматривать случай, когда х-2≥0 не нужно и пункт а) отпадает . Решаем сразу первое неравенство с пункта b) . Как видно по ответу, решением заданной системы является решение системы b) .

ivantretyak02

Алгебра

4,5(31 оценок)

(x-0,5)(x+2)³+(0,5-x)(x-1)³=9x-4,5 (x-0,5)(x+2)³-(x-0,5)(x-1)³-9(x-0,5)=0 (x-0,5)·((x+2)³-(x-1)³-9)=0 [/tex] (x-0,5)·(x+2-(x-1))·((x+2)²+(x+2)(x-1)+(x-1)²-9)=0 (x-0,5)·(x+2-x+1)·(x²+4x+4+x²+2x-x-2+x²-2x+1-9)=0 (x-0,5)·3·(3x²+6x-6)=0 (x-0,5)·9·(x²+2x-2)=0 x-0,5=0 или х²+2х-2=0 х=0,5 d=4+8=12 x=(-2-√12)/2 =-1-√3 или х=(-2+√12)/2 =-1+√3 среднее арифметическое корней (0,5+( -1-√3)+( -1+√3))/3=-1,5/3=-0,5 ответ. -0,5

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.