Регистрация Спросить otvet5GPT
zozoshcka17
04.06.2022 20:51
Алгебра
Есть ответ 👍

До іть будь ласка. Дуже потрібно

185
309
Посмотреть ответы 3

Ответы на вопрос:

Еденорожка666
Еденорожка666
4,4(84 оценок)

Кутовий коеффіцієнт прямої, перпендикулярної до даної, дорівнює 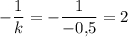-\dfrac{1}{k}=-\dfrac{1}{-0{,}5}=2

Знайдемо, в якій точці похідна дорівнює двом:

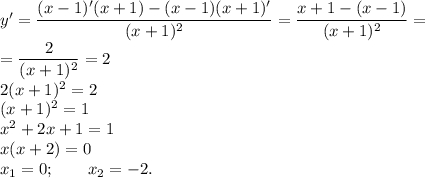
y'=\dfrac{(x-1)'(x+1)-(x-1)(x+1)'}{(x+1)^2}=\dfrac{x+1-(x-1)}{(x+1)^2}=\\=\dfrac{2}{(x+1)^2}=2\\2(x+1)^2=2\\(x+1)^2=1\\x^2+2x+1=1\\x(x+2)=0\\x_1=0; \qquad x_2=-2.

Перший випадок: x=0. Знайдемо значення функції:

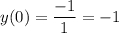
y(0)=\dfrac{-1}{1}=-1

Рівняння прямої з кутовим коефіцієнтом має вигляд:

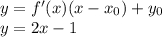
y=f'(x)(x-x_0)+y_0\\y=2x-1

Другий випадок x=-2:

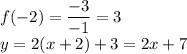
f(-2)=\dfrac{-3}{-1}=3\\y=2(x+2)+3=2x+7


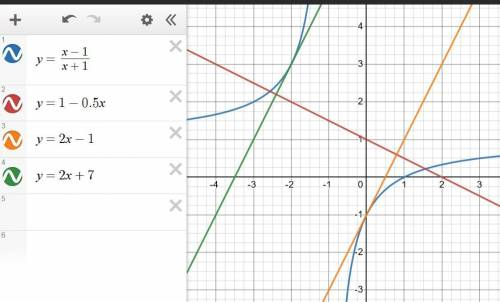
До іть будь ласка. Дуже потрібно
Demix485
Demix485
4,4(27 оценок)

Вітаю.

Відповідь:

Пояснення: фото


До іть будь ласка. Дуже потрібно
ghhgbg
ghhgbg
4,8(22 оценок)
Синус  возрастает на [-π/2;   π/2],  убывает  на [π/2;   3π/2] косинус возрастает  на  [0;   π], убывает [π;   2π] sin(-5π/12) - угол лежит в 4 четверти, где синус возрастает sin(5π/24) - угол лежит в 1 четврети, синус возрастает sin(17π/6) = sin(π - π/6) = sin(π/6) - угол лежит в 1 четверти, синус возрастает. когда функция возрастает, то большему значению аргумента соответствует большее значение функции, значит: -5π/12 < π/6 < 5π/24 sin(-5π/12) < sin(17π/6) < sin(5π/24) cos(13π/24) - угол лежит во 2 четверти, косинус возрастает. синус  смещен  относительно косинуса на π/2. 5π/24  <   13π/24 13π/24 + π/2 = 25π/24, cos(13π/24)  =  sin(25π/24)  = -sin(π/24) = sin(-π/24) > sin(-5π/12) ответ: sin(-5π/12)   <   cos(13π/24)  < sin(17π/6) < sin(5π/24)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS