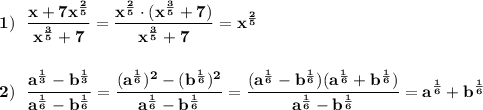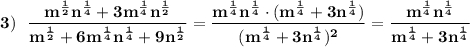Ответы на вопрос:
1.а) 2(х-32) б) 3(х+9)
2.б) 9х квадрат - 4
3. 462= 33,4631
Объяснение:
другие не смогла
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Розв язати рівняння (3х+4)(2х-9)=х(6х-3)-4...
 Q666Princess666Q10.01.2020 14:43
Q666Princess666Q10.01.2020 14:43 -
Освободите дробь от знака корня в знаменателе....
 DEGoP08.06.2022 13:29
DEGoP08.06.2022 13:29 -
решить учи ру желтальено...
 TatyanaKras01.07.2020 08:29
TatyanaKras01.07.2020 08:29 -
Cos^2(90+a) + cos^2(180-a) + tg (270-a)×tg(180+a)...
 Vita081422.11.2021 05:32
Vita081422.11.2021 05:32 -
Знайдіть найбільше і найменше значення виразу 6cos2_a_)-a-3sin2a...
 Nikita2033022.02.2023 08:32
Nikita2033022.02.2023 08:32 -
там на время с алгеброй...
 Гениально104.03.2020 15:07
Гениально104.03.2020 15:07 -
Найти значение выражения x2−2x+1приx=−10...
 lddobroz08.01.2020 08:27
lddobroz08.01.2020 08:27 -
6. Найдите диапазон значения функции ( )...
 gorkylush18.11.2020 20:23
gorkylush18.11.2020 20:23 -
Дано вибірку 7,5,4,6,4,3,8,5,4. Знайти її рохмах, моду, медіану і середнє значення....
 Savcik07.09.2020 23:07
Savcik07.09.2020 23:07 -
Упростить выражение (x¹⁵:x³)²•x⁴ ...
 Mogolan16.12.2022 07:31
Mogolan16.12.2022 07:31

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

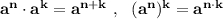 и формулы сокращённого умножения:
и формулы сокращённого умножения: 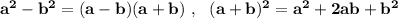 .
.