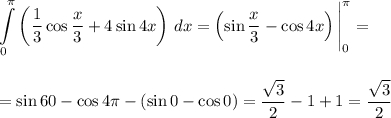Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
На доске выписаны числа 1; 16; 56 и 256. На каждом шаге разрешается...
 Dacha07K28.02.2022 03:06
Dacha07K28.02.2022 03:06 -
Число -3 є коренем рівняння а)5х-15=0 б)2y-12=0 в)3х+9=0 г)7у-14=0...
 qwelsaqwelsa18.08.2021 15:37
qwelsaqwelsa18.08.2021 15:37 -
І вариант 1. Разложите на множители: а) х^2 – 49; б) 36х^2 - y^2,...
 liyamenkova03.07.2021 01:40
liyamenkova03.07.2021 01:40 -
баллов Что означает найти пересечение множеств?...
 Tashernaut16.02.2020 09:35
Tashernaut16.02.2020 09:35 -
Наименьшее общее делимое 59049и729 32768и512...
 соннышко19.07.2020 21:47
соннышко19.07.2020 21:47 -
X²-x-72=0 имеет два корня 1) 2)x²+x²...
 BNN1103.12.2022 23:30
BNN1103.12.2022 23:30 -
Определи степень уравнений 2х-4у+6=0 5у^2-3х=0 -5ху=0 2(3х+4)+12=5у...
 krylovadashenk23.08.2021 04:56
krylovadashenk23.08.2021 04:56 -
решить, вообще не понпмаю как это, боже...
 Uliana4444117.09.2021 17:15
Uliana4444117.09.2021 17:15 -
1) x²+5-2√x²+5=3 2) ³√x²-3+ ^6√x²-3=2 3) x²-7=√x+1 ...
 05Artur1002.06.2022 20:06
05Artur1002.06.2022 20:06 -
Реши систему уравнений методом подстановки: x−2y=−2 7x−12y=7 ОТВЕТ...
 kseniyapolozhe12.12.2021 15:03
kseniyapolozhe12.12.2021 15:03

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.