Регистрация Спросить otvet5GPT
ASLiza1992
29.03.2021 14:50
Математика
Есть ответ 👍

: а) Решите уравнение cos²x-cos2x=1/2
б) Найдите все корни этого уравнения, принадлежащие отрезку [3P/2;3P]

110
173
Посмотреть ответы 3

Ответы на вопрос:

AleksaKiki
AleksaKiki
4,7(4 оценок)

А) cos²х- cos2х=1/2, используя основное тригонометрическое тождество и косинус двойного угла получаем

(1-sin²х) - (1- 2sin²х )=1/2,

sin²х=1/2,

sinх=√1/2, х= π/4+2πn , х= 5π/4+2πn

и

sinх=-√1/2 ,х=- π/4+2πn , х= -5π/4+2πn.

Объединим корни

х= π/4+2πn и х= -5π/4+2πn ⇒

х= π/4+πn, n∈Z.

Объединим корни

х= -π/4+2πn и х= 5π/4+2πn ⇒

х=-π/4+πn, n∈Z.

ответ . а) = π/4+πn, n∈Z, х= -π/4+πn, n∈Z.

Б) Лучше делать отбор корней на единичной окружности. Здесь представлен другой отбора для [3π/2;3π].

1) 3π/2 ≤ π/4+πn≤3π|(- π/4),

5π/4 ≤ πn≤11π/4 |:π ,

5/4 ≤ n≤11/4 , n∈Z ⇒

n=2, х1= π/4+π*2= 9π/4.

2) 3π/2 ≤ -π/4+πn≤3π|(+ π/4),

7π/4 ≤ πn≤13π/4 |:π ,

7/4 ≤ n≤13/4 , n∈Z ⇒ n=2,3

х2= -π/4+π*2=7π/4, х2== -π/4+π*3=11π/4.

ответ б) 7π/4, 9π/4, 11π/4.

DetaRUSION
DetaRUSION
4,4(100 оценок)

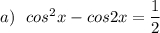
a)\ \ cos^2x-cos2x=\dfrac{1}{2}  

Формулы: 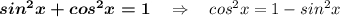  \boldsymbol{sin^2x+cos^2x=1}\ \ \ \Rightarrow \ \ \ cos^2x=1-sin^2x  ,

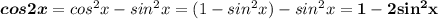
                   \boldsymbol{cos2x}=cos^2x-sin^2x=(1-sin^2x)-sin^2x=\bf 1-2sin^2x}    

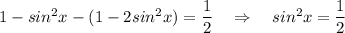
1-sin^2x-(1-2sin^2x)=\dfrac{1}{2}\ \ \ \Rightarrow \ \ \ sin^2x=\dfrac{1}{2}  

Применим формулу понижения степени : 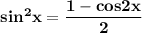  \bf sin^2x=\dfrac{1-cos2x}{2}   .

При применении этой формулы не потребуется думать над тем, как объединять корни в единую серию решений .

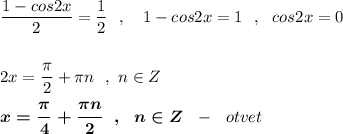
\dfrac{1-cos2x}{2}=\dfrac{1}{2}\ \ ,\ \ \ 1-cos2x=1\ \ ,\ \ cos2x=02x=\dfrac{\pi}{2}+\pi n\ \ ,\ n\in Zboldsymbol{x=\dfrac{\pi}{4}+\dfrac{\pi n}{2}\ \ ,\ \ n\in Z}\ \ -\ \ otvet  

б)   Отберём корни, принадлежащие заданному отрезку .  x\in \Big[\ \dfrac{3\pi }{2}\ ;\ 3\pi \ \Big]    

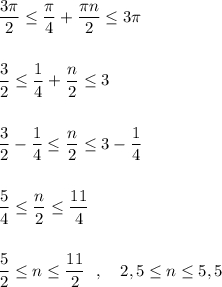
 \displaystyle \frac{3\pi}{2}\leq \dfrac{\pi}{4}+\dfrac{\pi n}{2}\leq 3\pi frac{3}{2}\leq \frac{1}{4}+\frac{n}{2}\leq 3frac{3}{2}-\frac{1}{4}\leq \frac{n}{2}\leq 3-\frac{1}{4}frac{5}{4}\leq \frac{n}{2}\leq \frac{11}{4}frac{5}{2}\leq n\leq \frac{11}{2}\ \ ,\ \ \ 2,5\leq n\leq 5,5  

Так как  n - целое , 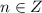 n\in Z  , то  n  может принимать значения 3 , 4 , 5 .

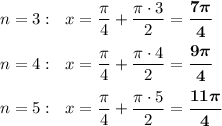
n=3:\ \ x=\dfrac{\pi}{4}+\dfrac{\pi \cdot 3}{2}=\boldsymbol{\dfrac{7\pi }{4}}n=4:\ \ x=\dfrac{\pi}{4}+\dfrac{\pi \cdot 4}{2}=\boldsymbol{\dfrac{9\pi }{4}}n=5:\ \ x=\dfrac{\pi}{4}+\dfrac{\pi \cdot 5}{2}=\boldsymbol{\dfrac{11\pi }{4}}

Даник1111112
Даник1111112
4,4(21 оценок)
Правельный ответ  2) сияет солнце

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS