aniavetisa

07.06.2023 12:51

Математика

Есть ответ 👍

Докажите равенство треугольников по медиане и по углам, на которые медиана разбивает угол треугольника

185

224

Посмотреть ответы 2

Ответы на вопрос:

jcgddrMarins

Математика

4,4(91 оценок)

***

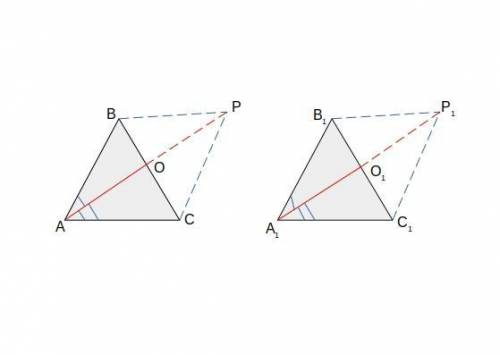
сделаем дополнительное построение

треугольник АВС

с точки О проведем отрезок ОР _ равной АО

с точки В - отрезок ВР

с точки С - отрезок СР

треугольник А₁В₁С₁

точно так же и

с точки О₁ проведем отрезок О₁Р₁ _ равной А₁О₁ ( равной и АО, и ОР )

с точки В₁ - отрезок В₁Р₁ _ равной ВР

с точки С₁ - отрезок С₁Р₁ _ равной СР

и так,

∠АОС = ∠ВОР _ как вертикальные углы

поскольку АО медиана

⇔

BО = ОС

АО = ОР

получается что

ΔADC = ΔDBK по первому признаку равенства треугольников (равенство треугольников по двум сторонам и углу между ними)

∠ОAC = ∠ОРB

АС = BK

⇔

ΔA₁О₁C₁ = ΔО₁B₁Р₁

∠О₁A₁C₁ = ∠О₁Р₁B₁

А₁С₁ = B₁Р₁

В треугольниках AВР и A₁B₁Р₁:

AР = A₁Р₁ поскольку AР = 2AО = A1Р1

∠ВAР = ∠B₁A₁K₁ _ по условию

∠BРA = ∠B₁K₁A₁ _ поскольку ∠BРA = ∠РAC = ∠Р₁A₁C₁ = ∠B₁Р₁A₁

∠KAC = ∠K1A1C1 _по условию

получается что треугольники ABР и ΔA₁B₁Р₁ по второму признаку равенства треугольников

(равенства треугольников по стороне и две прилежащих к ней угла)

значит:

АВ = А₁В₁

BР = B₁Р₁ = А₁С₁ = АС

Так как в треугольниках АВС и А₁В₁С₁

ВА = В₁А₁

АС = А₁С₁

∠ВAС = ∠В₁A₁С₁

⇔

ΔАВС = ΔA₁В₁С₁

по первому признаку равенства треугольников:

ответ: равенства треугольников _ доказано.

Докажите равенство треугольников по медиане и по углам, на которые медиана разбивает угол треугольни

IvanBur2006

Математика

4,4(24 оценок)

Сигарети спиртное і т.д

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.