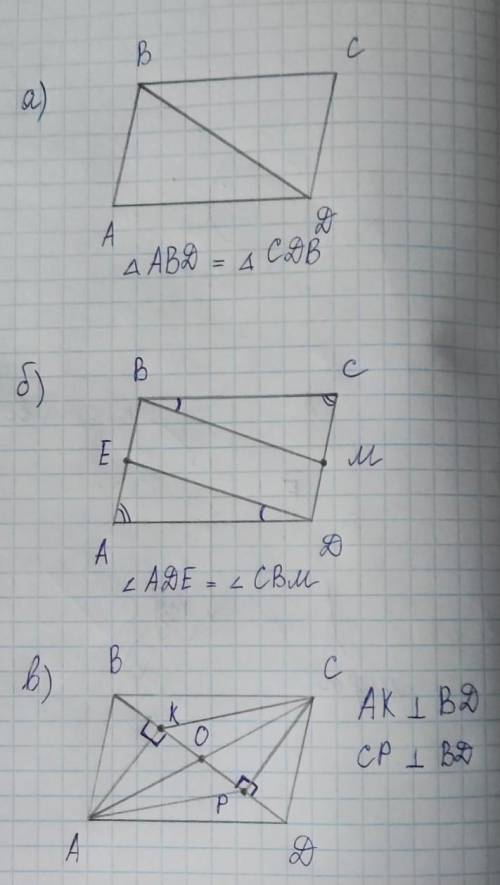
1. а) Діагональ BD ділить чотири кутник ABCD на рівні трикутники ABD і CDB. Довести, що ABCD - паралелограм. 6) На сторонах AB і CD паралелограма ABCD позначено вiдповiдно точки Е і М так, що <ADE=<CВМ. Довести, що BEDM паралелограм.

B) У паралелограмі ABCD на дiагоналі BD позначено точки К i P так, що АК перпендикулярно BD, CP перпендикулярно BD. До вести, що АКСР також є паралелограмом.

187

448

Посмотреть ответы 3

Ответы на вопрос:

kwasmarianna

Геометрия

4,7(33 оценок)

щиро вибачаюсь за якість (

1. а) Діагональ BD ділить чотири кутник ABCD на рівні трикутники ABD і CDB. Довести, що ABCD - парал

Рооопапооугвр

Геометрия

4,5(48 оценок)

Объяснение:

а) Из равенства треугольников имеем: AB = CD и AD = BC. Это значит, что стороны четырехугольника попарно равны, поэтому он и является параллелограммом.

б) AD = BC как стороны параллелограмма, <ADE = <CBM по условию, а <А = <С как противоположные углы параллелограмма, это значит, что ∆CMB = ∆AED. Из этого следует, что ED = BM. AE = CM (из равенства треугольников), значит EB = DM.

Из этого следует, что четырехугольник BEDM - параллелограмм.

в) Дополнительно проведем диагональ AC, которая является диагональю и для четырехугольника AKCP. AO = OC и BO = OD по свойству параллелограмма ABCD. <CPD = <AKB = 90°. CD = AB по свойству параллелограмма, AK = CP как перпендикуляры. Из вышеперечисленного следует, что ∆CPD = ∆AKB. Из равенства треугольников: BK = PD. KO = OB - BK, PO = OD - DP, поскольку OD = OB, а DP = BK, то PO = OB - BK, следовательно OK = OP. Диагонали четырехугольника AKCP делятся точкой пересечения пополам, поэтому AKCP - параллелограмм.

Gbdngggvg

Геометрия

4,8(58 оценок)

на фото по компьютору

Объяснение:

это пример как находить квадрат

Как найти квадрат высоты в прямоугольном треугольнике

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.