Регистрация Спросить otvet5GPT
rusnc
27.08.2020 05:32
Алгебра
Есть ответ 👍

решить задачу , очень , прощу вас

212
477
Посмотреть ответы 2

Ответы на вопрос:

nikfdd
nikfdd
4,7(79 оценок)

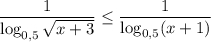
\dfrac{1}{\log_{0{,}5}\sqrt{x+3}} \le\dfrac{1}{\log_{0{,}5}(x+1)}

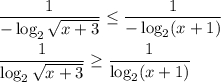
\dfrac{1}{-\log_2\sqrt{x+3}}\le \dfrac{1}{-\log_2(x+1)}dfrac{1}{\log_2 \sqrt{x+3}}\ge \dfrac{1}{\log_2(x+1)}\\

Пусть 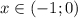x \in (-1;0). Тогда левый логарифм положителен, а правый отрицателен. Если мы домножим обе части неравенства на произведение логарифмов, неравенство сменит знак:

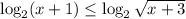
\log_2(x+1) \le \log_2\sqrt{x+3}

Логарифм с основанием, большим единицы, — монотонно возрастающая функция, поэтому:

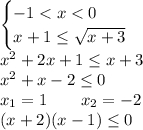
\begin{cases}-1 < x < 0\\x+1 \le \sqrt{x+3}\end{cases}\\x^2+2x+1\le x+3\\x^2+x-2\le0\\x_1=1 \qquad x_2=-2\\(x+2)(x-1)\le 0

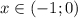Методом интервалов получим, что x \in [-2;1]. Объединяя с первым условием, получим: x \in (-1;0).

Пусть теперь 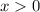x 0. Тогда, когда мы умножим обе части неравенства на произведение логарифмов, неравенство сохранит знак:

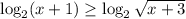
\log_2(x+1) \ge \log_2 \sqrt{x+3}

Проделываем всё то же самое:

\begin{cases}x 0\\ x+1 \ge \sqrt{x+3}\end{cases}\\x^2+2x+1 \ge x+3\\x^2+x-2\ge 0\\(x+2)(x-1) \ge 0\\x \in (-\infty; -2] \cup[1;+\infty)

Подходит только правый интервал:

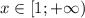
x \in [1;+\infty)

ответ: 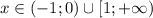x \in (-1;0)\cup[1;+\infty)

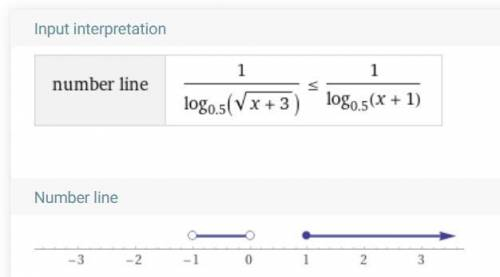
На скриншоте проверка на компьютере.

Если что-нибудь непонятно — спрашивай.


решить задачу , очень , прощу вас
taisia20061
taisia20061
4,5(92 оценок)
Это одна дробь? у меня вышло х+5/2х(•1)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS