НУЖНО СЕГОДНЯ В прямокутному паралелепіпеді 1111 AB = 12, AD = 5, 1 = 20.
Через ребро 11 під кутом 60° до площини основи ABCD проведено переріз.
Знайдіть площу цього перерізу.

141

278

Посмотреть ответы 2

Ответы на вопрос:

нина503

Геометрия

4,4(61 оценок)

Площадь сечения равна 120

Объяснение:

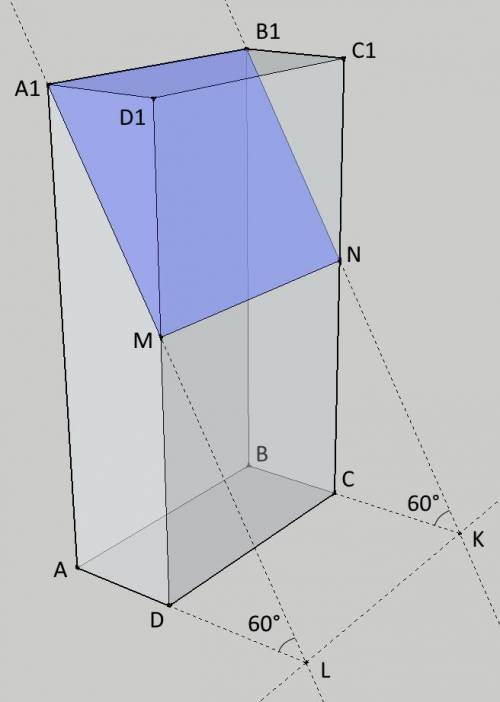
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB = 12, AD = 5, AA1 = 20. Через ребро A1B1 под углом 60° к плоскости основания ABCD проведено сечение. Найдите площадь этого сечения.

Прямая сечения, проведенная из точки A1 пересекает прямую AD в некоторой точке L, причем ∠A1LA = 60°.

Прямая сечения, проведенная из точки B1 пересекает прямую BC в некоторой точке K, причем ∠B1KB = 60°.

ΔA1LA и ΔB1KB прямоугольные и равны (AA1=BB1).

AL = AA1/tg(60°) = 20/√3 ≈ 11.5 > AD

А значит прямая A1L пересекает DD1 в некоторой точке M, образуя прямоугольный ΔA1D1M. ∠D1A1M = ∠A1LA = 60° как накрест лежащие при параллельных прямых AD и A1D1.

Аналогично находим точку N - пересечение B1K с прямой CC1.

ΔA1D1M = ΔB1C1N

Четырехугольник сечения A1B1NM является прямоугольником, одна сторона которого A1B1 = 12. Длину второй стороны A1M надо найти из треугольника A1D1M:

A1M = A1D1/cos(60°) = 5/(1/2) = 10

Площадь сечения будет равна:

SA1B1NM = A1B1*A1M = 12*10 = 120.

#SPJ1

НУЖНО СЕГОДНЯ В прямокутному паралелепіпеді 1111 AB = 12, AD = 5, 1 = 20. Через ребро 11 під кутом

Love2111

Геометрия

4,5(34 оценок)

180° - 55° - 63° = угол b

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.