Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Берілген тақ саннуң келесі тақ санмен қосындысы 36-дан кіші.соңғы...
 Настён198931.05.2021 07:41
Настён198931.05.2021 07:41 -
Диаметр окружности равен 4 5/11 м. вычислите длину окружности...
 Eg0rMirn9y28.07.2022 03:35
Eg0rMirn9y28.07.2022 03:35 -
Выполните сложение 3 кг 870 г + 4 кг 256 г...
 alisha15sherban16.07.2020 03:21
alisha15sherban16.07.2020 03:21 -
Диагональ ac параллелограмма abcd пересекает высоту be в точке...
 knyazik200328.05.2022 21:37
knyazik200328.05.2022 21:37 -
Вмагазине канцтоваров продаётся 140 цветных карандашей из 19...
 AnaDanik07.03.2021 06:31
AnaDanik07.03.2021 06:31 -
Верно ли, что если: 1) |х| 20,то-10 х+10 30; 2) |х| или=5,то-50...
 Артём8953501436705.06.2022 12:13
Артём8953501436705.06.2022 12:13 -
Построить в ля бемоль мажоре t53 s64 d6 t53...
 Людина509.09.2022 13:23
Людина509.09.2022 13:23 -
1) 18÷272)75÷183)76÷204)28÷175)9÷13надо с остатком ...
 Дмитртй1116.03.2022 02:38
Дмитртй1116.03.2022 02:38 -
Выбери и запиши числа ,которые: 1)делеться на 4,2)деляться на...
 buchelnikova8408.05.2023 21:35
buchelnikova8408.05.2023 21:35 -
Бір тігінші 18 көйлек ал екіншісі осындай 16 көйлек тікті екінші...
 flag410.05.2023 16:15
flag410.05.2023 16:15

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

 .
. .
.![log_{\sqrt[4]{7}}169=a\ \ \ \Rightarrow \ \ \ log_{7^{\frac{1}{4}}}13^2=\dfrac{2}{1/4}\cdot log_{7}\, 13=a\ \ ,\ \ log_7\, 13=\dfrac{a}{8}\ ;](/tpl/images/4977/6495/8edac.png)
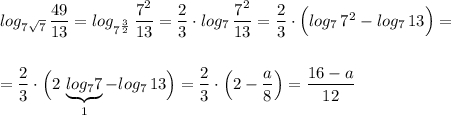
![log_{\sqrt[4]{2}}\sqrt{7}=a\ \ \Rightarrow \ \ \ log_{2^{\frac{1}{4}}}\, 7^{\frac{1}{2}}=\dfrac{4}{2}\cdot log_2\, 7=a\ \ ,\ \ log_2\, 7=\dfrac{a}{2}\ ;](/tpl/images/4977/6495/784a2.png)
![log_{2\sqrt[3]{2}}\, \dfrac{7}{16}=log_{2^{\frac{4}{3}}}\dfrac{7}{2^4}=\dfrac{3}{4}\cdot log_2\, \dfrac{7}{2^4}=\dfrac{3}{4}\cdot \Big(log_27-log_2\, 2^4\Big)==\dfrac{3}{4}\cdot \Big(\dfrac{a}{2}-4\cdot log_22\Big)=\dfrac{3}{4}\cdot \Big(\dfrac{a}{2}-4\Big)=\dfrac{3\, (a-8)}{8}](/tpl/images/4977/6495/1f04a.png)