черныйхащ

11.06.2020 20:18

Геометрия

Есть ответ 👍

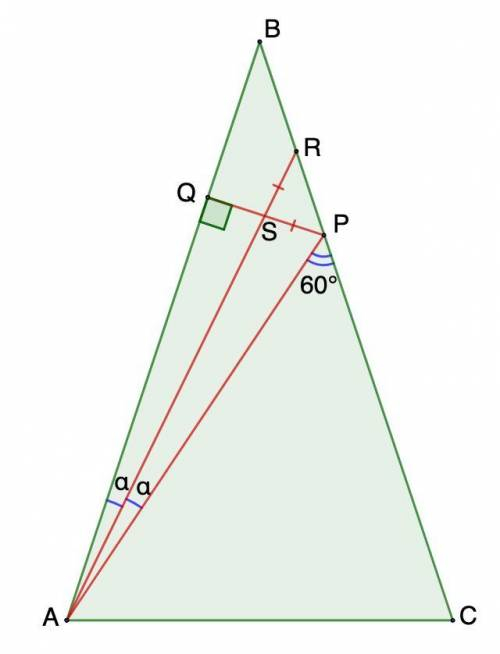
Дан равнобедренный треугольник ABC (AB = BC). Точка P на стороне BC такова, что угол APC = 60градусов. Высота PQ и биссектриса AR треугольника APB пересекаются в точке S. Оказалось, что PS = SR. Чему равен угол ABC?

267

338

Посмотреть ответы 2

Ответы на вопрос:

ZEWER

Геометрия

4,5(43 оценок)

Угол АВС равен 40°.

Объяснение:

Дан равнобедренный треугольник ABC (AB = BC). Точка P на стороне BC такова, что угол APC = 60°. Высота PQ и биссектриса AR треугольника APB пересекаются в точке S. Оказалось, что PS = SR. Чему равен угол ABC?

Дано: ΔАВС - равнобедренный;

Р ∈ ВС, ∠APC = 60°;

PQ - высота, AR - биссектриса ΔАРВ;

PQ ∩ AR = S;

PS = SR.

Найти: ∠АВС.

Пусть ∠BAR = ∠RAP = α (AR - биссектриса ΔАРВ)

1. Рассмотрим ΔARP.

∠APC = 60° - внешний.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

⇒ ∠ARP = 60° - α

2. Рассмотрим ΔABP.

∠APC = 60° - внешний.

⇒ ∠ABC = 60° - 2α (1)

3. Рассмотрим ΔSRP.

PS = SR (условие)

⇒ SRP - равнобедренный.

Углы при основании равнобедренного треугольника равны.

⇒ ∠SPR = ∠ARP = 60° - α

4. Рассмотрим ΔQBP.

PQ - высота ΔАРВ.

⇒ ΔQBP - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АВС = 90° - ∠SPR = 90° - 60° + α = 30° + α (2)

5. Приравняем выражения (1) и (2) и найдем α:

60° - 2α = 30° + α

3α = 30°

α = 10°

⇒ ∠АВС = 30° + α = 30° + 10° = 40°.

Угол АВС равен 40°.

Дан равнобедренный треугольник ABC (AB = BC). Точка P на стороне BC такова, что угол APC = 60градусо

W1LDOR

Геометрия

4,7(15 оценок)

ответ:8,85Объяснение:Диаметр = 17,7Радиус=17,7:2=8,85Диаметр = 2*Радиус

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.