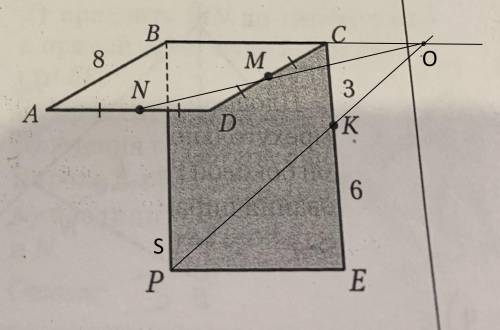
abcd - ромб. BCD - прямоугольник. найдите длину отрезка по которой плоскость mnk пересекает прямоугольник BCEP

281

339

Посмотреть ответы 2

Ответы на вопрос:

Hutorttt

Геометрия

4,8(45 оценок)

Объяснение:

Проведем прямую BC и MN до точки пересечения (они обе лежат в плоскости ромба ABCD). Точку пересечения обозначим O.

Теперь проведем прямую OK, она пересечет прямую BP в некоторой точке S.

Рассмотрим треугольники DMN и CMO. В них углы DMN и CMO - вертикальные, поэтому равны, CM = MD по условию, углы MND и MOC - накрест лежащие при параллельных прямых, а значит тоже равны.

Треугольники DMN и CMO равны по двум углам и стороне, а значит CO = DN = AB/2 = 8/2 = 4.

Треугольник KCO - прямоугольный с прямым углом C и катетами CK = 3, CO = 4 - египетский треугольник, KO = 5.

Рассмотрим треугольники BOS и COK, BS параллельна CK, треугольники подобны, коэффициент подобия:

BO/CO = (8+4)/4 = 3

Тогда:

BS = CK*3 = 3*3 = 9

BS = BP следовательно точка пересечения прямой OK с прямой BP (S) совпадает с точкой P.

OP = OK*3 = 15

KP = OP-OK = 15-5 = 10

abcd - ромб. BCD - прямоугольник. найдите длину отрезка по которой плоскость mnk пересекает прямоуго

QuAtTro271

Геометрия

4,6(34 оценок)

∠c=∠a=30 - в равнобедренном тр углы при основании равны. ∠b=180-2*30=120. ab=bc=x; s=(1/2)ab*bc*sin∠b = (1/2)x²*sin120; x²=2s/sin120= 2*16√3 / (√3/2) = 64; x=8. проводим высоту вн. bh=ab/2=4 - как катет против угла 30° в тр. авн. по теореме пифагора ah=√(ab²-bh²)= √(64-16)=√48=4√3. ac=2*ah=8√3, т. к. высота в равнобедренном тр. является и медианой. находим периметр: p=ab+bc+ac=8+8+8v3=8(2+v3).

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.