Алгебра: Найти количество корней уравнения на отрезке

mgam56

26.09.2022 04:30

Алгебра

Есть ответ 👍

Найти количество корней уравнения на отрезке

264

266

Посмотреть ответы 3

Ответы на вопрос:

nastyasiminyuk

Алгебра

4,7(75 оценок)

2) 2

Объяснение:

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

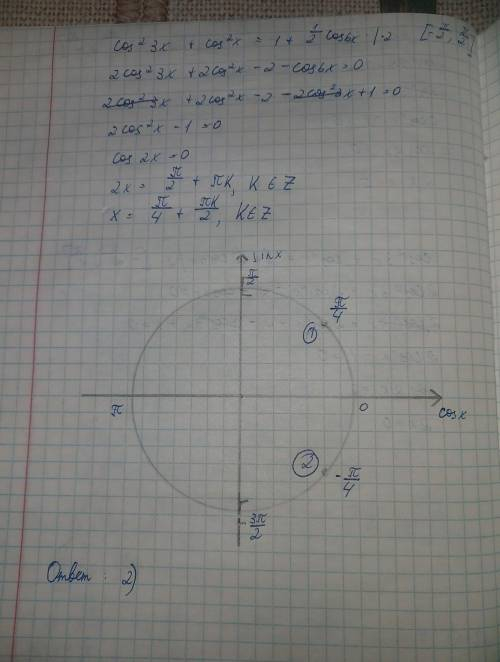
Найти количество корней уравнения на отрезке

Marii111

Алгебра

4,8(61 оценок)

Уравнение на отрезке [ -π/2 ; π/2 ] имеет два корня

x₁ = -π/4

x₂ = π/4

Объяснение:

Найдите количество корней уравнения

cos² 3x + cos² x = 1 + 1/2 · cos6x на отрезке [ -π/2 ; π/2 ]

Воспользуемся формулой понижения степени

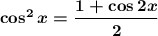
$\boldsymbol{ \cos ^2 x = \dfrac{1 + \cos 2x}{2} }$

Подставим в исходное уравнение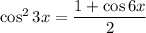

$\cos ^2 3x = \dfrac{1 + \cos 6x }{2}$

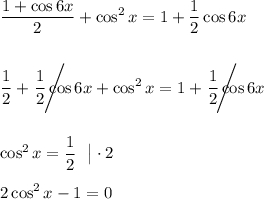
$\displaystyle \dfrac{1 + \cos 6x }{2} + \cos ^2 x = 1 + \dfrac{1}{2} \cos 6x \frac{1}{2} + ~~ \Bigg \slash \!\!\!\!\!\!\!\!\!\!\!\dfrac{1}{2} \cos 6x + \cos ^2 x = 1 + ~~ \Bigg \slash \!\!\!\!\!\!\!\!\!\!\!\dfrac{1}{2} \cos 6x \cos ^2 x = \frac{1}{2} ~~ \big |\cdot 2 2\cos ^2 x - 1= 0$

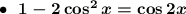
$\bullet ~~ \boldsymbol{1 -2\cos ^2 x = \cos 2x}$

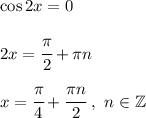
$\cos 2 x =0 2x = \cfrac{\pi }{2} + \pi n x=\cfrac{\pi }{4} + \cfrac{\pi n}{2} ~, ~ n \in \mathbb Z$

Находим корни принадлежащие отрезку

$\left [ -\dfrac{\pi }{2 } ~ ; ~ \dfrac{\pi }{2} ~ \right ]$

При n = -2

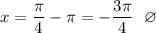
$x = \dfrac{\pi }{4} -\pi = -\dfrac{3\pi }{4} ~~ \varnothing$

При n = -1

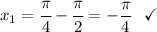
$x_1=\cfrac{\pi }{4} - \cfrac{\pi }{2 } = -\dfrac{\pi }{4} ~~\checkmark$

При n = 0

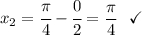
$x_2=\cfrac{\pi }{4} - \cfrac{0}{2 } = \dfrac{\pi }{4} ~~\checkmark$

При n = 1

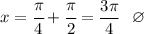
$x=\cfrac{\pi }{4} + \cfrac{\pi }{2 } = \dfrac{3\pi }{4} ~~\varnothing$

Выходит , что на данном отрезке уравнение имеет два корня

SmartJager

Алгебра

4,6(9 оценок)

А) ограничена снизу б) наибольшее=8, наименьшее=0 в) f(0)=2*0²=0 f(-1)=2*(-1)²=2 f(3)=2*(3)²=18

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.