Ответы на вопрос:
Відповідь:
1) х=5, у=3 или (5;3)
2) х=5, у=-3 или (5;-3)
3) 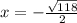 ,
, 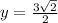 или
или 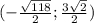
4) 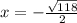 ,
, 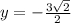 или
или 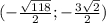
Пояснення:
Сначала нужно бы найти ОДЗ, но мы потом сделаем проверку, что бы исключить ненужные корни.
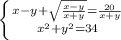
Как видим, в первом уравнении есть в знаменатели х+у и корень из х+у.
Что бы от него избавится, умножим первое уравнение на х+у, считая что х+у положительное значение (что бы внести под корень) .
А из второго выразим х²
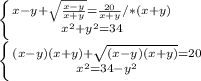
В первом уравнении получилась формула (х-у)(х+у)=х²-у²
А потом заменим х² на 34-у²
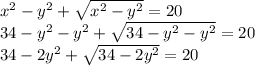
Сделаем замену переменных 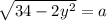
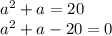
У нас получилось квадратное уравнение с коэффициентами a=1, b=1, c=-20
Найдем сначала дискриминант по формуле: 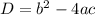 , а потом и корни уравнения по формулах
, а потом и корни уравнения по формулах 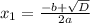 и
и 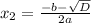
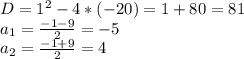
Теперь возвращаемся к замене переменных:
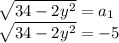 (Так как корень не может быть отрицательным числом, то этот вариант нам не подходит)
(Так как корень не может быть отрицательным числом, то этот вариант нам не подходит)
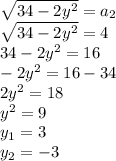
Еще раз возвращаемся до того момента, когда мы х² выражали через у²
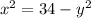
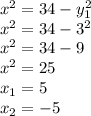
Такие же корни будут при (-3), поскольку в квадрате минус исчезнет, и будет то же что и с 3 в квадрате!
Теперь у нас есть 4 разных значения, и нужно сделать проверку на ОДЗ для всех возможных значений. Сначала будем проверять, не отрицательное значение ли под корнем, а затем все остальное.
1) х=5, у=3
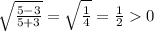
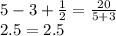
Такая пара корней нам подходит (5;3)
2) х=5, у=-3
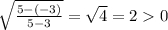
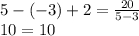
Такая пара корней нам подходит (5;-3)
3) х=-5, у=-3
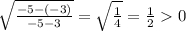
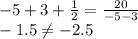
Такая пара корней нам не подходит
4) х=-5, у=3
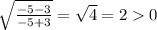
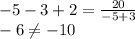
Такая пара корней нам не подходит
Теперь, что бы избавится от знаменателя, умножим первое уравнение на -(х+у), считая что х+у отрицательное значение (что бешим.
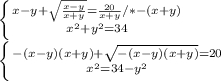
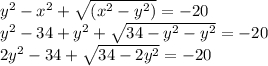
Сделаем замену переменных 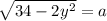
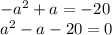
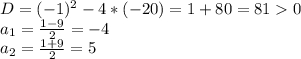
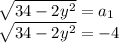 (Так как корень не может быть отрицательным числом, то этот вариант нам не подходит)
(Так как корень не может быть отрицательным числом, то этот вариант нам не подходит)
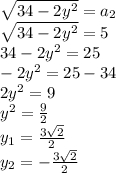
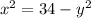
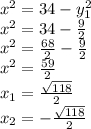
Нам подойдут только пары, которые меньше нуля:
Только 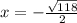 и
и 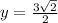
и 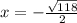 и
и 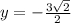
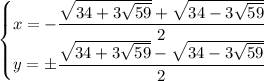
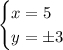
Объяснение:
Чтобы уравнение было менее страшным, введём новые обозначения.
Обозначим x + y = u.
Чтобы было проще извлечь корень
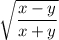
удобно обозначить x - y = uv², причем для определённости примем v ≥ 0. Тогда весь корень равен просто v.
Решение первого уравнения.Рассмотрим, что получится, если подставить новые переменные в первое уравнение:
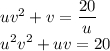
После замены переменных t = uv получается квадратное уравнение t² + t = 20, корни которого угадываются по теореме Виета, это t = -5 или t = 4.
Итак, uv = -5 или uv = 4. Тогда x - y = uv · v = -5v или 4v.
Первый случай. x - y = -5vПоскольку по договоренности v ≥ 0, u должно быть отрицательным.
Заметим, что (x - y)² + (x + y)² = x² - 2xy + y² + x² + 2xy + y² = 2(x² + y²) = 68 в соответствии со вторым уравнением. Тогда, подставив новые переменные, получаем:
u² + 25v² = 68
При этом u² · 25v² = 25(uv)² = 25², значит по теореме Виета u² и 25v² — корни квадратного уравнения t² - 68t + 25² = 0.
Выделяем полный квадрат: t² - 68t + 25² = t² - 2 · 34t + 34² + (25² - 34²) = (t - 34)² + (25 - 34)(25 + 34) = (t - 34)² - 9 · 59
Значит, t = 34 ± 3√59 — оба корня положительные. Получаем два варианта:
1) 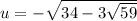 ,
, 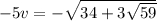 . В терминах x и y это приводит к такой системе уравнений:
. В терминах x и y это приводит к такой системе уравнений:
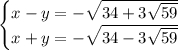
Полусумма и полуразность этих уравнений даёт x и y
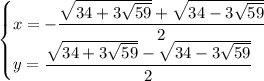
2) 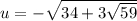 ,
, 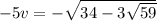 . Аналогично,
. Аналогично,
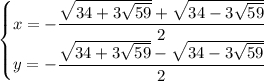
Здесь u должно быть положительным. Следуя первому случаю, последовательно находим:
u² + 16v² = 68
При этом u² · 16v² = 16(uv)² = 16², значит по теореме Виета u² и 16v² — корни квадратного уравнения t² - 68t + 16² = 0.
Выделяем полный квадрат: t² - 68t + 16² = t² - 2 · 34t + 34² + (16² - 34²) = (t - 34)² + (16 - 34)(16 + 34) = (t - 34)² - 30²
Значит, t = 34 ± 30, t = 4 или t = 64. Получаем два варианта:
1) u = 2, 4v = 8. В терминах x и y это приводит к такой системе уравнений:
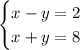
Решение этой системы уравнений — x = 5, y = 3
2) u = 8, 4v = 2. Аналогично, x = 5, y = -3.
ПостскриптумРешения для "первого случая" (когда x - y = -5v) выглядят громоздко. В принципе, их можно оставить и так, но можно немного упростить.
Попробуем извлечь корень, возможно это как-то . Положим
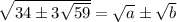
Возведём в квадрат:
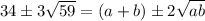
Чтобы равенство выполнялось, достаточно потребовать
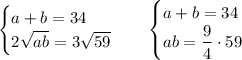
Еще раз вспоминаем теорему Виета, a и b оказываются корнями уравнения
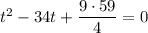
Корни этого уравнения 9/2 и 59/2. Так как 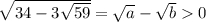 , то a должно быть больше b. Значит,
, то a должно быть больше b. Значит,
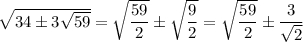
Если подставить полученные значения вместо корней в решение для первого случая, получится пара корней
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
нужна . кто ответит верно, ставлю оценку + сердечко (выбрать правильный...
 Irakrasnova7202.03.2020 19:27
Irakrasnova7202.03.2020 19:27 -
2х³-3х²-4х+5-х²+5х-6 УМОЛЯЮ...
 liz04128.08.2021 20:31
liz04128.08.2021 20:31 -
Решить уравнение: x²-x-6=0 x²=2x+8 25x²-1=0 2x²-10x=0...
 AlinaSki11.05.2022 10:54
AlinaSki11.05.2022 10:54 -
.Упростите выражение –4 (2,5а – 1,5) + 5,5а – 8. Найдите его значение...
 IrishkaKoteika268923.05.2021 02:30
IrishkaKoteika268923.05.2021 02:30 -
Визначте скільки розв язків має система рівнянь...
 вова99309.01.2023 20:26
вова99309.01.2023 20:26 -
Знайди суму и різницю дробів:...
 ILYA342104.10.2020 14:41
ILYA342104.10.2020 14:41 -
. Помножте одночлен на многочлен: а) а(2а+3); б) 3х(х²-4х+3); в) -2b(b²+2b-3);...
 Милаха788443305.02.2021 20:16
Милаха788443305.02.2021 20:16 -
11. Укажите значения х, при которых график функции у = х2 – 7х – 18 лежит...
 витя5534615.12.2021 17:27
витя5534615.12.2021 17:27 -
При каких значениях с выражение 11с/с+7 не имеет смысла?...
 полмвзсгдчэлжпчхмэвп25.02.2020 08:09
полмвзсгдчэлжпчхмэвп25.02.2020 08:09 -
Тест 1 заполните пропуски (многоточия), чтобы получилось верное высказывание....
 nestann17.09.2022 02:24
nestann17.09.2022 02:24

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
