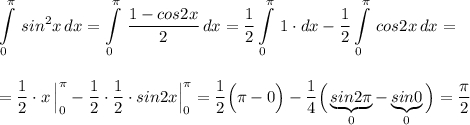Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Алгебра 8класс номер 28...
 петя21213.09.2020 12:37
петя21213.09.2020 12:37 -
І.102. Представьте степень в виде произведения: 1) (xy): 3) (0, 25т n );...
 froze199713.11.2021 22:03
froze199713.11.2021 22:03 -
Решите уравнение в натуральных числах НОК (х^2, y) + НОК (х, у^2) = 1996...
 хадЯ6605.01.2022 16:20
хадЯ6605.01.2022 16:20 -
Сколько будет? можете с решением а)3/11×22/45= ...
 maloyzolotov26.08.2020 01:54
maloyzolotov26.08.2020 01:54 -
-те сделать СОР по алгебре...
 Elena40700823.04.2023 20:05
Elena40700823.04.2023 20:05 -
При каких значениях x двучлен 5x−4 принимает отрицательные значения? (В...
 Blazethecat21822.06.2020 04:36
Blazethecat21822.06.2020 04:36 -
решить надо сдать до 13:00,умоляю!!!...
 193934515.09.2020 12:22
193934515.09.2020 12:22 -
Найдите моду, медиану и середину выборки: 1) 4, 3, 2, 0, 3, -2; 2) 6, 5,...
 helpmepleasehelp104.04.2020 07:13
helpmepleasehelp104.04.2020 07:13 -
решить систему, до 12:00 надо уже отправить учителю...
 nikita124710.01.2023 23:03
nikita124710.01.2023 23:03 -
Прочтите текст. Цена на алюминий 1 апреля составляла 123 200 рублей за тонну....
 eegorov199604.04.2020 08:54
eegorov199604.04.2020 08:54

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

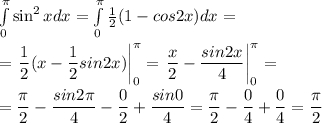
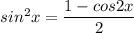 .
.