Регистрация Спросить otvet5GPT
lllGlitcherlll
05.01.2022 17:29
Математика
Есть ответ 👍

Даны множества A = {(x, y)| x2 + y2 = 4, x, y ∈ R} и
B = {(x, y)| x − y = 2, x, y ∈ R}. Определите
множество A ∩ B.

251
363
Посмотреть ответы 2

Ответы на вопрос:

PokerFresh
PokerFresh
4,6(51 оценок)

Множество A ∩ B состоит из двух точек (0, -2) и (2, 0); A ∩ B = {(0, -2), (2, 0)}

Пошаговое объяснение:

Пересечение двух множеств A и B (обозначается A ∩ B) образуют элементы, которые входят в A и в B одновременно.

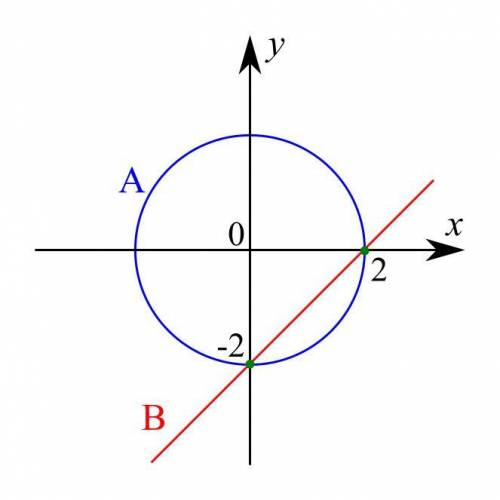
Поскольку в первое множество входят все пары чисел (x, y), удовлетворяющие условию x² + y² = 4, а во второе — условию x - y = 2, то A ∩ B — все пары (x, y), удовлетворяющие системе из двух уравнений

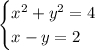
\begin{cases}x^2+y^2=4\\x-y=2\end{cases}

Остаётся решить эту систему уравнений. Это можно сделать графически или аналитически.

Аналитическое решение

Возведём второе уравнение в квадрат (получится x² - 2xy + y² = 4) и вычтем полученное из первого уравнения.

Тогда 2xy = 0, откуда x = 0 или y = 0.

Если x = 0, то, поскольку x - y = 2, y = x - 2 = 0 - 2 = -2; (0, -2) — первая точка, входящая в пересечение.

Если y = 0, то x = y + 2 = 2; (2; 0) —  вторая точка.

Графическое решение

Первое уравнение системы (его удобно переписать в виде x² + y² = 2²) задаёт на плоскости Oxy окружность с центром в начале координат и радиусом 2.

Второе уравнение задаёт прямую, для построения которой достаточно знать две точки. Подойдут, например, (0, -2) и (2, 0).

Пересечение множеств, которые заданы линиями на плоскости, — просто пересечение этих линий.

Окружность и прямая пересекаются в двух точках (0, -2) и (2, 0). Эти точки и составляют искомое пересечение.


Даны множества A = {(x, y)| x2 + y2 = 4, x, y ∈ R} и B = {(x, y)| x − y = 2, x, y ∈ R}. Определите м
egorik2506
egorik2506
4,6(10 оценок)

по отношению к первой семье вторая платит на  (350-250)*100%/250=10000/250=40%

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS