Регистрация Спросить otvet5GPT
лерчик1253
29.11.2022 04:18
Математика
Есть ответ 👍

Кто может решить, не проходите мимо
УРАВНЕНИЕ:

191
230
Посмотреть ответы 2

Ответы на вопрос:

ната1187
ната1187
4,7(85 оценок)

Пошаговое объяснение:

\sqrt{5x^2+24x+28}-\sqrt[3]{5x^2+24x+27}\leq 1 .

ОДЗ:

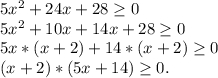
5x^2+24x+28\geq 0\\5x^2+10x+14x+28\geq 0\\5x*(x+2)+14*(x+2)\geq 0\\(x+2)*(5x+14)\geq 0.

-∞__+__-2,8__-__-2__+__+∞

x∈(-∞;-2,8]U[-2;+∞).

Пусть: \sqrt[6]{5x^2+24x+28} =t\geq 0\ \ \ \ \ \Rightarrow\\

t^3-(t-1)^2\leq 1\\t^3-(t^2-2t+1)-1\leq 0\\t^3-t^2+2t-1-1\leq 0\\t^3-t^2+2t-2\leq 0\\t^2*(t-1)+2*(t-1)\leq 0\\(t-1)*(t^2+2)\leq 0\\t^2+2 0\ \ \ \ \Rightarrow\\t-1\leq 0\\t\leq 1\\t\geq 0\ \ \ \ \Rightarrow\\0\leq t\leq 1\ \ \ \ \ \Rightarrow\\\left \{ {{t\geq 0} \atop {t\leq 1}} \right. \ \ \ \ \ \left \{ {{\sqrt[6]{5x^2+24x+28}\geq 0 } \atop {\sqrt[6]{5x^2+24x+28}\leq 1 }} \right. \ \ \ \ \ \left \{ {{(\sqrt[6]{5x^2+24x+28})^6\geq 0^6 } \atop {(\sqrt[6]{5x^2+24x+28})^6\leq 1^6 }} \right.

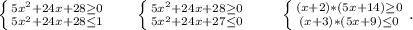
\left \{ {5x^2+24x+28\geq 0} \atop {5x^2+24x+28\leq 1}} \right. \ \ \ \ \ \left \{ {5x^2+24x+28\geq 0} \atop {5x^2+24x+27\leq 0}} \right.\ \ \ \ \ \ \left \{ {{(x+2)*(5x+14)\geq 0} \atop {(x+3)*(5x+9)\leq 0}} \right. .

1. (x+2)*(5x+14)≥0

-∞__+__-2,8__-__-2__+__+∞

x∈(-∞;-2,8]U[-2;+∞).

2. (x+3)*(5x+9)≤0

-∞__+__-3__-__-1,8__+__+∞

x∈[-3;-1,8].          ⇒

x∈[-3;-2,8]U[-2;-1,8].

Учитывая ОДЗ     ⇒

ответ: x∈[-3;-2,8]U[-2;-1,8].


Кто может решить, не проходите мимо УРАВНЕНИЕ:
Кто может решить, не проходите мимо УРАВНЕНИЕ:
olegtab34
olegtab34
4,8(66 оценок)
1км = 1000м 140км 50м = 140×1000+50 = 140 050м

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS