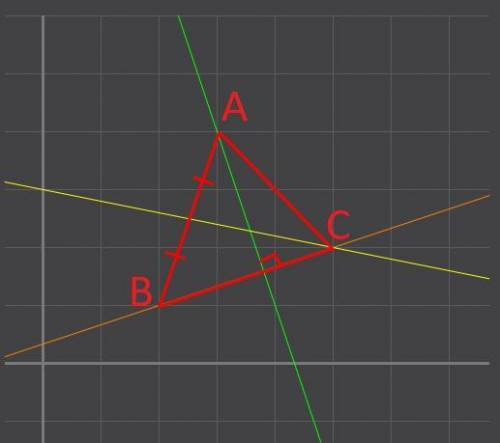
В треугольнике ABC A(3; 4 ) В(2;1) С(5;2)
составьте
уравнения:
1) стороны BC
2) высоты, опущенной из вершины Aна сторону BC
3) медианы, проведенной из вершины C .
177
320
Ответы на вопрос:
1. Для нахождения уравнения стороны ВС воспользуемся уравнением прямой, проходящей через две точки 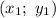 и
и 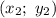 :
:
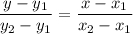
Эти две точки: 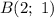 и
и 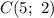 . Получим:
. Получим:
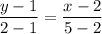
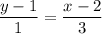
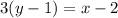
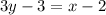
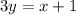
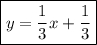
2. Высота АН является перпендикулярной к прямой ВС. Угловые коэффициенты перпендикулярных прямых являются обратными противоположными числами. Так как 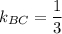 , то
, то 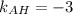 . Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом:
. Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом:
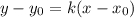
Точка 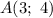 , угловой коэффициент
, угловой коэффициент 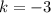 . Получим:
. Получим:
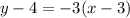
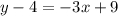
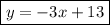
3. Найдем середину М отрезка АВ. Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка:
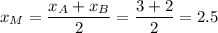
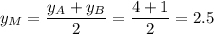
Вновь воспользуемся уравнением прямой, проходящей через две точки: 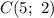 и
и 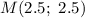 .
.
Получим:
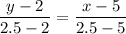
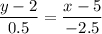
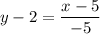
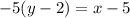
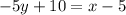
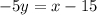
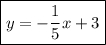
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Как решить столбиком пример 11970 разделить на 400...
 Grigoof21.11.2020 22:13
Grigoof21.11.2020 22:13 -
Написать проект.на тему фигуры..2 класс...
 Пирожочек0708.04.2022 11:17
Пирожочек0708.04.2022 11:17 -
Одна бригада рабочих делает за12 дней 1512 деталей, другая -1260.сколько...
 Viki388812.07.2020 13:12
Viki388812.07.2020 13:12 -
Ширина прямокутника 8 см, а довжина - у 4 рази більша. чому дорівнює...
 pechka50906.02.2021 14:56
pechka50906.02.2021 14:56 -
Как разделить пирог прямоугольной формы на 4 части, чтобы получилось...
 StepanEgorov14.06.2023 03:48
StepanEgorov14.06.2023 03:48 -
В11 часов из аэропорта одновременно в противоположных направлениях...
 АндрейTV106.03.2020 15:51
АндрейTV106.03.2020 15:51 -
Вырази длину в метрах. 40дм,160дм,700дм,850дм,600см,1000дм...
 Rigina198406.04.2020 22:01
Rigina198406.04.2020 22:01 -
Из двух городов, расстояние между которыми 600ем, вышли одновременно...
 dilyahashimova24.11.2022 21:28
dilyahashimova24.11.2022 21:28 -
Решить туристы прошли за 2 дня 48 км,причём в первый день на 10...
 boriskina200609.11.2021 16:57
boriskina200609.11.2021 16:57 -
Вычислить только тебе суммы в которых одно слагаемое на 10 больше...
 фракталы12.08.2020 22:13
фракталы12.08.2020 22:13

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
