Алгебра: До іть 1). cosx -√2/2 2)tgx≥-1 3)tg(4x+π/4)+1≤0

djasiclol

06.03.2023 13:19

Алгебра

Есть ответ 👍

До іть
1). cosx<-√2/2
2)tgx≥-1
3)tg(4x+π/4)+1≤0

207

497

Посмотреть ответы 2

Ответы на вопрос:

ренатик9

Алгебра

4,4(88 оценок)

1) ответ : { π/4 + 2πk < x < 7π/4 + 2πk , k € Z }

2) ответ: { (-π/4) + πk ; π/2 + πk }

3) ответ: { (-3π/16) + πk/4 ; (-π/8) + πk/4 )

Объяснение:

Формулы:

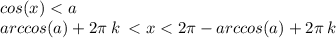
$cos(x) < a \\ arccos(a) + 2\pi \: k \: < x < 2\pi - arccos(a) + 2\pi \: k \:$

где k € Z

$tg(x) \geqslant a$

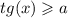
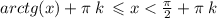
$arctg(x) + \pi \: k \: \leqslant x < \frac{\pi}{2} + \pi \: k \:$

где k € Z

$tg(x) \leqslant a \\ \\ - \frac{\pi}{2} + \pi \: k \leqslant x < arctg(a) + \pi \: k$

где k € Z

$\cos(x) < \frac{ \sqrt{2} }{2}$

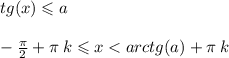
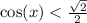
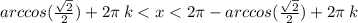
$arccos( \frac{ \sqrt{2} }{2} ) + 2\pi \: k < x < 2\pi - arccos( \frac{ \sqrt{2} }{2} ) + 2\pi \: k$

где k € Z

$\frac{\pi}{4} + 2\pi \: k \: < x < 2\pi - \frac{\pi}{4} + 2\pi \: k \:$

где k € Z

$\frac{\pi}{4} + 2\pi \: k \: < x < \frac{7\pi}{4} + 2\pi \: k \:$

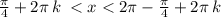
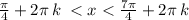
где k € Z

ответ : { π/4 + 2πk < x < 7π/4 + 2πk , k € Z }

$tg(x) \geqslant - 1$

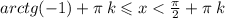
$arctg( - 1) + \pi \: k \leqslant x < \frac{\pi}{2} + \pi \: k \:$

где k € Z

$( - \frac{\pi}{4} ) + \pi \: k \leqslant x < \frac{\pi}{2} + \pi \: k \:$

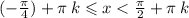
где k € Z

ответ: { (-π/4) + πk ; π/2 + πk }

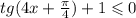
$tg(4x + \frac{\pi}{4} ) + 1 \leqslant 0$

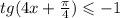
$tg(4x + \frac{\pi}{4} ) \leqslant - 1$

ЗАМЕНА (4x + π/4) = a

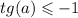
$tg(a) \leqslant - 1$

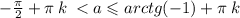
$- \frac{\pi}{2} + \pi \: k \: < a \leqslant arctg( - 1) + \pi \: k \:$

где k € Z

$- \frac{\pi}{2} + \pi \: k \: < a \leqslant ( - \frac{\pi}{4} ) + \pi \: k \:$

где k € Z

$- \frac{\pi}{2} + \pi \: k < 4x + \frac{\pi}{4} \leqslant ( - \frac{\pi}{4} ) + \pi \: k$

где k € Z

$- \frac{\pi}{2} - \frac{\pi}{4} + \pi \: k \: < 4x \leqslant ( - \frac{\pi}{4} ) - \frac{\pi}{4} + \pi \: k \:$

где k € Z

$( - \frac{3\pi}{4} ) + \pi \: k \: < 4x \leqslant ( - \frac{2\pi}{4} ) + \pi \: k \:$

где k € Z

$( - \frac{3\pi}{16} ) + \frac{\pi \: k}{4} < x \leqslant ( - \frac{\pi}{8} ) + \frac{\pi \: k \: }{4}$

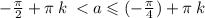
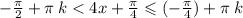
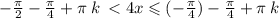
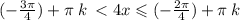
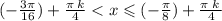
где k € Z

ответ: { (-3π/16) + πk/4 ; (-π/8) + πk/4 )

Undina705

Алгебра

4,6(94 оценок)

А) (х-4)^2 б) (2а+3в)^2

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

juliyakam
06.02.2022 19:35

График функции y=k/x проходит через точку а(10;.6) проходит ли график этой...
pstrebykina
01.01.2021 09:10

первый член бесконечно убывающей геометрической прогрессии с положительными...
demeshkin1
26.07.2022 15:29

Определи общий множитель выражения z+6d(z+b)+b....
Тунгышбаева82
08.12.2021 01:58

Помагите x²-y=7 x²y=18...
zelenkadi
05.12.2022 21:06

24.3-задание. Вычислите: 1) C (сверху) 4 (снизу) 8+ C (сверху) 3 (снизу) 8=...
miha1lovkirill
15.07.2020 14:19

Установите соответствие между количеством решений системы линейных уравнений...
nastyaivanko09
19.09.2021 17:22

Известно, что в арифметической прогрессии a_1 = 12,8; S_30 = 1080. Найдите...
Aigerim800
13.09.2022 21:21

Проверочная работа решение треугольников. В треугольнике ABC угол A равен 45...
merhanoooI
19.08.2020 21:06

N2-9m2 . 16n2-9m2 • n- +6mn+9m² 16n2-24mn+9m2...
Dashasvi
31.01.2020 01:25

Укажить пару яка е розвязком ривняня 2x+3y=7...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.