Математика: ТЕМА ЧАСТИННІ ПОХІДНІ ДО ІТЬ ІВ

Nagoshka

25.10.2021 14:04

Математика

Есть ответ 👍

ТЕМА ЧАСТИННІ ПОХІДНІ ДО ІТЬ ІВ

232

459

Посмотреть ответы 2

Ответы на вопрос:

pashafil5

Математика

4,6(85 оценок)

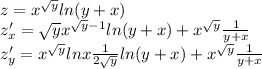
$z = {x}^{ \sqrt{y} } ln(y + x) \\ z'_{x} = \sqrt{y} {x}^{ \sqrt{y} - 1 } ln(y + x) + {x}^{ \sqrt{y} } \frac{1}{y + x} \\ z'_{y} = {x}^{ \sqrt{y} } lnx \frac{1}{2 \sqrt{y} } ln(y + x) + {x}^{ \sqrt{y} } \frac{1}{y + x}$

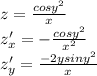
$z = \frac{ {cosy}^{2} }{x} \\ z'_{x} = - \frac{ {cosy}^{2} }{ {x}^{2} } \\ z'_{y} = \frac{ - 2y {siny}^{2} }{x}$

Пошаговое объяснение:

похідні по х і у першої функції це похідна добутку, щоб знайти таку похідну треба знайти суму: друга функція помножити на похідну першої функції плюс перша функція помножити на похідну другої функції

спочатку знайдемо похідну z по х значить у тут в ролі сталої, тобто шукаємо як похідну хⁿ і дописуємо другу функцію з логарифмом, потім шукаємо похідну від логарифма і дописуємо х^√у,

якщо z' по у, то тут х в ролі сталої, шукаємо похідну (а^х)'=а^хlnа і оскільки тут √у то ще треба записати похідну від кореня і дописати ln(y+x) і другий додаток такий же як в похідні по х

похідна по х і у другої функції це звичайна похідна в першому випадку це (1/х)'=-1/х² але замість одиниці записуємо cosy², в другому випадку треба знайти похідну (cosy²)'=-siny²×(у²)'=-2уsiny² і дописати 1/х як сталу

ilyavarbanetsozotem

Математика

4,7(35 оценок)

646573аав

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.