парасат3

29.12.2021 22:27

Математика

Есть ответ 👍

Ученик написал сочинение по теме «Треугольники». Вот некоторые фрагменты его сочинения 1. Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
2. Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.
3. Площадь любого треугольника можно вычислить по формулам:
S=1/2* ah и S= 1/2 ab* sinC
4. Если в треугольник вписана окружность, то его площадь можно найти по формуле S= abc/4R , где радиус этой окружности вычисляется по теореме косинусов: R= a/2cosA.
5. А если около треугольника описать окружность, то для нахождения площади
треугольника справедлива формула S = (a + b + c)*r .
6. Прямая, параллельная стороне треугольника, является его средней линией.
7. Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.
Все ли верно в сочинении ученика? Напишите , ошибки и правильный вариант.

275

461

Посмотреть ответы 2

Ответы на вопрос:

Ника6660

Математика

4,5(70 оценок)

Пошаговое объяснение:

1. Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.

Приемлемо, однако следует добавить, что эти три точки не лежат на одной прямой.

2. Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.

Это неверно. И медианой, и высотой является только биссектрисса угла, противолежащего основанию, а не любая.

3. Площадь любого треугольника можно вычислить по формулам:

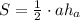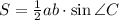$S=\frac{1}{2}\cdot ah_a$ и $S= \frac{1}{2} ab\cdot \sin\angle C$ .

Верно.

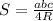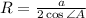4. Если в треугольник вписана окружность, то его площадь можно найти по формуле $S= \frac{abc}{4R}$ , где радиус этой окружности вычисляется по теореме косинусов: $R= \frac{a}{2\cos\angle A}$ .

Неверно. Речь идет про описанную окружность, а не вписаную.

5. А если около треугольника описать окружность, то для нахождения площади треугольника справедлива формула 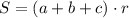$S = (a + b + c)\cdot r$

Здесь так же перепутаны вписанная и описанная окружности. Речь идет про вписанную окружности. К тому же ее радиус вычисляется по теореме синусов, а не косинусов.

6. Прямая, параллельная стороне треугольника, является его средней линией.

Неверно. Не всякая прямая, паралельная стороне треугольника является его средней линией. Можно дополнить тем, что прямая проходит через середину другой стороны, тогда это будет средняя линия.

7. Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.

В тексте приведен признак подобия треугольников, но не равенства. Не все прямоугольные треугольники подобны. Для подобия двух прямоугольных треугольников достаточно чтобы были равны два острых угла.

Исправленный вариант

Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками, не лежащими на одной прямой.

Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести биссектрису угла, противолежащего основанию, она будет являться медианой и высотой.

Площадь любого треугольника можно вычислить по формулам:

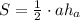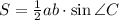$S=\frac{1}{2}\cdot ah_a$ и $S= \frac{1}{2} ab\cdot \sin\angle C$ .

Если около треугольника описана окружность, то его площадь можно найти по формуле 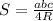$S= \frac{abc}{4R}$ , где радиус этой окружности вычисляется по теореме синусов: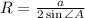 $R= \frac{a}{2\sin\angle A}$

А если в треугольник вписать окружность, то для нахождения площади треугольника справедлива формула 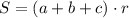$S = (a + b + c)\cdot r$ .

Прямая, параллельная стороне треугольника и проходящая через его середину, является его средней линией.

Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники подобны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники с парой равных острых углов подобны.

naziflashru

Математика

4,4(5 оценок)

,так как при a ⊂(π; 3π/2) cos(a) ⊂ (-1; 0) ответ: ctg(a)={1}

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.