mishasinik

24.01.2023 21:54

Математика

Есть ответ 👍

Отрезки PH и PF являются высотой и биссектрисой треугольника PQR соответственно. Известно, что угол PQR - угол PRQ = 22 градуса. Найдите угол , с объяснением и, если возможно, рисунком!

297

317

Посмотреть ответы 2

Ответы на вопрос:

abrashevamarin

Математика

4,6(36 оценок)

∠HPF = 11°.

Объяснение:

Отрезки PH и PF являются высотой и биссектрисой ΔPQR соответственно. Разность между величинами углов PQR и PRQ равна 22°. Найти угол HPF.

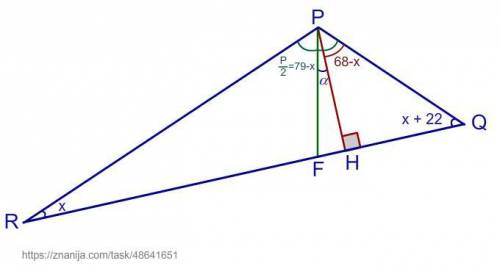
Дано: ΔPQR;

PH - высота;
PF - биссектриса;

∠PQR - ∠PRQ = 22°.

Найти: ∠HPF.

Решение.

1) По условию:

∠PQR - ∠PRQ = 22°.

⇒ ∠PQR = ∠PRQ + 22°.

Пусть ∠PRQ = x, тогда ∠PQR = x + 22°.

Сумма углов в треугольнике равна 180°

2) В ΔPQR

∠PRQ = x;

∠PQR = x + 22°;

∠QPR = 180° - x - (x + 22°) = 180° - x - x - 22° = 158 - 2x.

Биссектриса угла в треугольнике - это луч, с началом в вершине угла и делящий угол пополам.

3) По условию PF - биссектриса.
∠FPR = ∠QPF = ∠QPR : 2 = (158 - 2x) : 2 = 79 - x.

Высота - это перпендикуляр, проведенный из вершины треугольника на противоположную сторону.

4) PH - высота по условию.

ΔQPH прямоугольный. ∠PHQ = 90°, ∠PQH = x + 22°,

⇒ ∠QPH = 90° - (x + 22°) = 90° - x - 22° = 68° - x.

5) Для удобства обозначим угол между биссектрисой и высотой α.

∠HPF = α.

∠α = ∠QPF - ∠QPH;

∠α = 79 - x - (68 - x) = 79 - x - 68 + x = 11°

∠HPF = 11°.

Угол между биссектрисой и высотой равен 11°.

Отрезки PH и PF являются высотой и биссектрисой треугольника PQR соответственно. Известно, что угол

Yuliya475

Математика

4,6(95 оценок)

0,4 : 3 3/7 = х : 2,5, х = (0,4 * 2,5) / 3 3/7 = 1 : 3 3/7 = 1 : 24/7 = 1 * 7/24 = 7/24 - неизв. член проп

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.